一盒中有10个产品 其中有4个次品 6个正品 随机地抽取一个测试 测试后不放回 直到次品都找到．求最
一盒中有10个产品，其中有4个次品，6个正品，随机地抽取一个测试，测试后不放回，直到次品都找到．求最后一个次品在下列情况发现的概率： (1)在第5次测试时发现； (2)在第10次测试时发现．
请帮忙给出正确答案和分析，谢谢！
参考解答
492***444
2023-11-14 03:32:10
正确答案：(1)由于一个样本点是由5个不同产品组成的一个排列故样本点总数为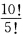
． 设A表示“在第5次测试日寸找到最后1个次品”．为计算A所包含的样本点的个数可考虑通过两步来完成：首先在前四次测试中有3个次品1个正品共有C43C61种不同的取法其次这4个产品有测试顺序的不同共有4 1种不同的排列方式两步搭配知A所包含的样本点的个数为C43C614 !．于是由(1．1)式有 
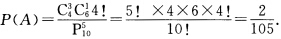． (2)由与(1)相同的分析知样本点总数为P1010=10!． 设B表示“在第10次测试时找到最后一个次品”A所包含的样本点的个数为C439 !于是得 
．
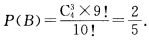(1)由于一个样本点是由5个不同产品组成的一个排列,故样本点总数为．设A表示“在第5次测试日寸找到最后1个次品”．为计算A所包含的样本点的个数,可考虑通过两步来完成：首先在前四次测试中有3个次品,1个正品,共有C43C61种不同的取法,其次这4个产品有测试顺序的不同,共有41种不同的排列方式,两步搭配知A所包含的样本点的个数为C43C614!．于是由(1．1)式有．(2)由与(1)相同的分析知样本点总数为P1010=10!．设B表示“在第10次测试时找到最后一个次品”,A所包含的样本点的个数为C439!,于是得．
相似问题
表示下列随机试验的随机事件 并分析它们之间的相互关系： (1)掷一颗骰子 记录掷得的点数 考虑事件：
表示下列随机试验的随机事件，并分析它们之间的相互关系： (1)掷一颗骰子，记录掷得的点数，考虑事件：“掷得的点数不超过2”，“掷得的点数不超过3”，
设随机变量X～N(μ σ2) 则方程y2+4y+X=0无实根的概率为 则μ=( )．A．1B．2C．
设随机变量X～N(μ，σ2)，则方程y2+4y+X=0无实根的概率为，则μ=( )．A．1B．2C．3D．4请帮忙给出正确答案和分析，谢谢！
保卫小组共有10人 每晚从10人中任意选派1人值夜班 以X表示某指定的1人在1周(7天)被派去值夜班
保卫小组共有10人，每晚从10人中任意选派1人值夜班，以X表示某指定的1人在1周(7天)被派去值夜班的次数，求X的分布律及其一周值班超过3次的概率．请帮忙给
设G是曲线y=2x—x2与x轴所围成的区域 在G内任取一点P P到y轴的距离为X 求X的分布函数和概
设G是曲线y=2x—x2与x轴所围成的区域，在G内任取一点P，P到y轴的距离为X，求X的分布函数和概率密度．请帮忙给出正确答案和分析，谢谢！
某人有5把钥匙 但忘记了开门的是哪一把 逐把试开 问： ①恰好第三次打开房门的概率是多少? ②三次内
某人有5把钥匙，但忘记了开门的是哪一把，逐把试开，问： ①恰好第三次打开房门的概率是多少? ②三次内打开房门的概率是多少? ③如5把中有2把房门钥匙
