设G是曲线y=2x—x2与x轴所围成的区域 在G内任取一点P P到y轴的距离为X 求X的分布函数和概
设G是曲线y=2x—x2与x轴所围成的区域，在G内任取一点P，P到y轴的距离为X，求X的分布函数和概率密度．
请帮忙给出正确答案和分析，谢谢！
参考解答
403***444
2023-11-14 03:11:31
正确答案：区域G的面积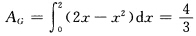 
由曲线y=2x—x2、直线x=t(0≤t≤2)及x轴所围成的区域(如图2．2所示)D的面积 
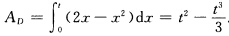．显然当f<0时 F(t)一P{X≤t=0当t≥2时 F(t)一P{X≤t)=1当0≤t＜2时 
．
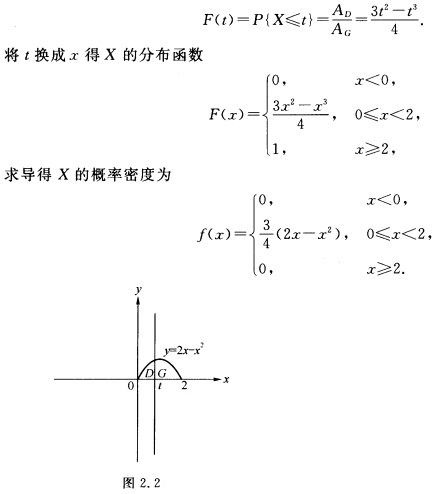这是一个用几何概型概率的计算方法，求连续型随机变量的分布的例题．为求分布函数在t(0≤t≤2)处的值，即求F(t)=P(X≤t)．由于事件{X≤t出现的充分必要条件是点P落在由曲线y=2x—x2、直线x=t及x轴所围的区域D上，因此P{X≤t)可用区域D的面积与G的面积之比计算．
相似问题
某人有5把钥匙 但忘记了开门的是哪一把 逐把试开 问： ①恰好第三次打开房门的概率是多少? ②三次内
某人有5把钥匙，但忘记了开门的是哪一把，逐把试开，问： ①恰好第三次打开房门的概率是多少? ②三次内打开房门的概率是多少? ③如5把中有2把房门钥匙
设随机变量X～b(n p) 即X的分布律为 P{X=k)=Cnkpk(1一p)n—k k=0 1 …
设随机变量X～b(n，p)，即X的分布律为 P{X=k)=Cnkpk(1一p)n—k，k=0，1，…，n，求k使得P{X=k}最大．请帮忙给出正确答案和分析，谢谢！
设随机变量X～N(0 1) 求y=2X2+1的概率密度．请帮忙给出正确答案和分析 谢谢！
设随机变量X～N(0，1)，求y=2X2+1的概率密度．请帮忙给出正确答案和分析，谢谢！
设电压V=A sin 其中A是一已知的正常数 相角～U(0 π) 试求电压V的概率密度．请帮忙给出正
设电压V=A sin，其中A是一已知的正常数，相角～U(0，π)，试求电压V的概率密度．请帮忙给出正确答案和分析，谢谢！
设随机变量X～π(λ)．即X的分布律为 P{X=k)= k=0 1 2 …． (1)求X取偶数的概率
设随机变量X～π(λ)．即X的分布律为 P{X=k)=，k=0，1，2，…． (1)求X取偶数的概率； (2)若P(X=2)=P{X=3}，求X取偶数的概率．请帮忙给出正确答案和分析，谢谢！
