设随机变量X～b(n p) 即X的分布律为 P{X=k)=Cnkpk(1一p)n—k k=0 1 …

正确答案：解不等式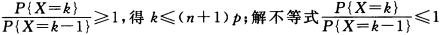得k≥(n+1)p． 如果(n+1)p为正整数当k＜(n+1)p时P{X=k)>P{X=k一1)．因此 P{X=(n+1)p一1)＞P{X=kk=01…(n+1)p一2；当k＞(n+1)p时P{X=k)＜P{X=k一1)．因此 P{X=(n+1)p)＞p{X=k)k=(n+1)p+1…n；当k=(n+1)p时有 P{X=(n+1)p)=P{X=(n+1)p一1可见如果(n+1)p为正整数当k=(n+1)p(n+1)p一1时P{X=k)取得最大值． 如果(n+1)p不是正整数当k＜(n+1)p时P{X=k)>P{X=k一1．因此 P{X=[(n+1)p＞P{X=k)k=01…[(n+1)p一1；当k＞(n+1)p时P{X=k)＜P{X=k一1．因此 P{X=[(n+1)p)＞P{X=k)k=[(n+1)p+1…n；可见如果(n+1)p不是正整数当k=[(n+1)p时P{X=k)取得最大值其中[(n+1)p表示(n+1)p的整数部分．
此题的k取值0，1，…，n，不宜用高等数学求连续变量函数的最大值的方法求解．一般求解的方法是解不等式．从而确定k为何值时，使得P{X=k)最大．