设A是素矩阵 则对任意的正整数m Am是素矩阵．请帮忙给出正确答案和分析 谢谢！

正确答案：因为γ(A)为A的单重特征值而且是A的模为γ(A)的唯一特征值所以(γ(A))^m。是A^m的单特征值而且是A^m的模为(γ(A))^m的唯一特征值．因此对m≥1由于有A^m≥0要证明A^m是素矩阵只需证明A^m是不可约的．用反证法．假定对某个正整数vA^v是可约的不妨设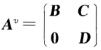其中BD为子方阵．设Ax=r(A)xx>0于是有A^vx=(γ(A))^vx对应于BD将x写成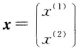从而有d^vx⁽²⁾=(γ(A))^vx⁽²⁾这表明(γ(A))^v是D的特征值． 另一方面再考虑A^T它也是非负的和不可约的那么必存在向量y>0使得A^Ty=γ(A)y．类似地可推出(γ(A))^v是B^T的特征值从而也是B的特征值． 这样(γ(A))^v是D的特征值又是B的特征值则γ(A)成了A的多重特征值矛盾!因此对所有的m≥1A^m是不可约的．从而A^m是素矩阵．
因为γ(A)为A的单重特征值,而且是A的模为γ(A)的唯一特征值,所以(γ(A))m。是Am的单特征值,而且是Am的模为(γ(A))m的唯一特征值．因此,对m≥1,由于有Am≥0,要证明Am是素矩阵,只需证明Am是不可约的．用反证法．假定对某个正整数v,Av是可约的,不妨设,其中B,D为子方阵．设Ax=r(A)x,x>0,于是有Avx=(γ(A))vx,对应于B,D,将x写成,从而有dvx(2)=(γ(A))vx(2),这表明(γ(A))v是D的特征值．另一方面,再考虑AT,它也是非负的和不可约的,那么必存在向量y>0,使得ATy=γ(A)y．类似地,可推出(γ(A))v是BT的特征值,从而也是B的特征值．这样,(γ(A))v是D的特征值又是B的特征值,则γ(A)成了A的多重特征值,矛盾!因此,对所有的m≥1,Am是不可约的．从而Am是素矩阵．