设函数y=f(x)在(一∞ +∞)内连续 在(一∞ 0)U(0 +∞)内二阶可导 其导函数的图像如右
设函数y=f(x)在(一∞，+∞)内连续，在(一∞，0)U(0，+∞)内二阶可导，其导函数的图像如右图，则y=f(x)在(一oo，+∞)内( )．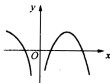 
A．有两个极大值，一个极小值，两个拐点
B．有两个极大值，一个极小值，一个拐点
C．有一个极大值，一个极小值，两个拐点
D．有一个极大值，一个极小值，一个拐点
请帮忙给出正确答案和分析，谢谢！
参考解答
463***102
2024-11-16 16:45:17
正确答案：A
导函数图象与x轴有三个交点，故有三个驻点．由第一充分条件知函数在三个驻点处从左至右依次取极大、极小、极大值．由于f'(x)有一个零点和一个不存在的点(x=0)，根据已知图形中f'(x)的单调性知在这两个点的左、右f'(x)异号，而f(x)在(一∞，+∞)内连续，所以函数图象有两个拐点．
相似问题
设对任意的x 总有φ(x)≤f(x)≤g(x) 且lim[g(x)一φ(x)]=0 则limf(x)
设对任意的x，总有φ(x)≤f(x)≤g(x)，且lim[g(x)一φ(x)]=0，则limf(x)( )．A．存在且等于零B．存在但不一定为零C．一定不存在D．不一定存在请帮忙给出
求下列函数的渐近线： 请帮忙给出正确答案和分析 谢谢！
求下列函数的渐近线： 请帮忙给出正确答案和分析，谢谢！
求下列函数的二阶偏导数： (1)z＝x4－3y3＋2xy； (2)z＝yx．请帮忙给出正确答案和分析
求下列函数的二阶偏导数： (1)z＝x4－3y3＋2xy； (2)z＝yx．请帮忙给出正确答案和分析，谢谢！
设f(x) g(x)在[a b]上存在二阶导数 且g〞(x)≠0 f(a)＝f(b)＝g(a)＝g(
设f(x)，g(x)在[a，b]上存在二阶导数，且g〞(x)≠0，f(a)＝f(b)＝g(a)＝g(b)＝0， 证明：(1)在开区间(a，b)内g(x)≠0； (2)在开区间(a，b)内至少存在一
求下列极限： 计算 其中D是由曲线y＝1／x 直线y＝x及x＝2所围成的区域．计算 其中D是由曲线y
求下列极限： 计算，其中D是由曲线y＝1／x，直线y＝x及x＝2所围成的区域．计算，其中D是由曲线y＝1／x，直线y＝x及x＝2所围成的区域．请帮忙给出正确答
