设f(x) g(x)在[a b]上存在二阶导数 且g〞(x)≠0 f(a)＝f(b)＝g(a)＝g(

正确答案：证明 (1)(反证法)假设存在点c∈(ab)使g(c)＝0则f(x)g(x)分别在区间[ac[cb上用罗尔定理得jε₁∈(ac)ε₂∈(cb)使得gˊ(ε₁)＝gˊ(ε₂)＝0进而再在区间[ε₁ε₂上对gˊ(x)再用罗尔定理知了ε₃∈(ε₁ε₂)使得g〞(ε₃)＝0；但这与题设g〞(x)≠0矛盾所以在开区间(ab)内g(x)≠0 (2)在开区间(ab)内至少存在一点ε使得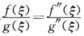 设F(x)＝f(x)gˊ(x)－fˊ(x)g(x)易知 F(a)＝f(a)gˊ(a)－fˊ(a)g(a)＝0 F(b)＝f(b)gˊ(b)－fˊ(b)g(b)＝0在[ab上对F(x)用罗尔定理 必存在ε∈(ab)使fˊ(ε)＝0 Fˊ(ε)＝Fˊ(x)｜_x＝ε＝[fˊ(x)gˊ(x)+f(x)g〞(x)－f〞(x)g(x)－fˊ(x)gˊ(x)｜_x＝ε ＝[f(x)g〞(x)－f〞(x)g(x)｜_x＝ε＝f(ε)g〞(ε)－f〞(ε)g(ε)＝0 又因为g(ε)≠0g〞(ε)≠0 所以 ε∈(ab)
证明(1)(反证法)假设存在点c∈(a,b),使g(c)＝0,则f(x),g(x)分别在区间[a,c,[c,b上用罗尔定理,得jε1∈(a,c),ε2∈(c,b),使得gˊ(ε1)＝gˊ(ε2)＝0,进而再在区间[ε1,ε2上对gˊ(x)再用罗尔定理知了ε3∈(ε1,ε2),使得g〞(ε3)＝0；但这与题设g〞(x)≠0矛盾所以在开区间(a,b)内g(x)≠0(2)在开区间(a,b)内至少存在一点ε,使得设F(x)＝f(x)gˊ(x)－fˊ(x)g(x),易知F(a)＝f(a)gˊ(a)－fˊ(a)g(a)＝0,F(b)＝f(b)gˊ(b)－fˊ(b)g(b)＝0,在[a,b上对F(x)用罗尔定理,必存在ε∈(a,b),使fˊ(ε)＝0Fˊ(ε)＝Fˊ(x)｜x＝ε＝[fˊ(x)gˊ(x)+f(x)g〞(x)－f〞(x)g(x)－fˊ(x)gˊ(x)｜x＝ε＝[f(x)g〞(x)－f〞(x)g(x)｜x＝ε＝f(ε)g〞(ε)－f〞(ε)g(ε)＝0又因为g(ε)≠0,g〞(ε)≠0所以ε∈(a,b)