设函数w=f(z)在｜z｜＜1内解析 且是将｜z｜＜1共形映射成｜w｜＜1的分式线性变换．试证 设在
设函数w=f(z)在｜z｜＜1内解析，且是将｜z｜＜1共形映射成｜w｜＜1的分式线性变换．试证 设在｜z｜＜1内f(z)解
设在｜z｜＜1内f(z)解析．且｜f(z)｜＜1；但f(a)=0(｜a｜＜1)．试证：在｜z｜＜1内，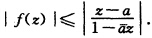 
请帮忙给出正确答案和分析，谢谢！
参考解答
463***102
2024-11-21 01:11:41
正确答案：w=φ(z)=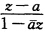
在｜z｜＜1内解析把｜z｜＜1映为｜w｜＜1且φ(a)=0它的反函数z=φ-1(w)在｜w｜＜1内解析把｜w｜＜1映为｜z｜＜1且φ-1(0)=a．于是复合函数F(w)=f[φ-1(w)在｜w｜＜1内解析｜F(0)｜=f[φ-1(0)=f(a)=0当｜w｜＜1时｜F(w)｜=｜f[φ-1(w)｜=｜f(z)｜＜1由施瓦茨引理｜F(w)｜≤｜w｜即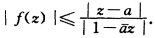
w=φ(z)=在｜z｜＜1内解析,把｜z｜＜1映为｜w｜＜1,且φ(a)=0,它的反函数z=φ-1(w)在｜w｜＜1内解析,把｜w｜＜1映为｜z｜＜1,且φ-1(0)=a．于是复合函数F(w)=f[φ-1(w)在｜w｜＜1内解析,｜F(0)｜=f[φ-1(0)=f(a)=0,当｜w｜＜1时,｜F(w)｜=｜f[φ-1(w)｜=｜f(z)｜＜1,由施瓦茨引理,｜F(w)｜≤｜w｜,即
相似问题
试判定下列函数 哪些是单值函数?哪些是多值函数? 请帮忙给出正确答案和分析 谢谢！
试判定下列函数，哪些是单值函数?哪些是多值函数? 请帮忙给出正确答案和分析，谢谢！
甲袋中有4个红球2个白球 乙袋中有2个红球．设从袋中取球时各球被取到的可能性相等．今从甲袋中任取一球
甲袋中有4个红球2个白球，乙袋中有2个红球．设从袋中取球时各球被取到的可能性相等．今从甲袋中任取一球放人乙袋中，再从乙袋中任取一球，则从乙袋中取到
关于独立性 下列说法中错误的是( )．A．若A1 A2 A3相互独立 则其中任意两个事件相互独立B．
关于独立性，下列说法中错误的是( )．A．若A1，A2，A3相互独立，则其中任意两个事件相互独立B．若A1，A2，A3相互独立，则其中任意两个事件的对立事件也
计算积分 设f(z)在｜z｜＜1内解析 在｜z｜≤1上连续 试证： 其中z属于C的内部．设f(z)在
计算积分 设f(z)在｜z｜＜1内解析，在｜z｜≤1上连续，试证： 其中z属于C的内部．设f(z)在｜z｜＜1内解析，在｜z｜≤1上连续，试证： 其中z属于C的
将下列函数在指定环域内展为洛朗级数． 将下列各函数在指定圆环内展为洛朗级数．将下列各函数在指定圆环内
将下列函数在指定环域内展为洛朗级数． 将下列各函数在指定圆环内展为洛朗级数．将下列各函数在指定圆环内展为洛朗级数． 请帮忙给出正确答案和分析，谢谢！
