假设矩阵A和B满足关系式AB＝A＋2B 其中已知A B为3阶矩阵 且满足2A－1B＝B一4E 其中E
假设矩阵A和B满足关系式AB＝A＋2B，其中已知A，B为3阶矩阵，且满足2A－1B＝B一4E，其中E是3阶单位矩阵．
已知A，B为3阶矩阵，且满足2A－1B＝B一4E，其中E是3阶单位矩阵． (1)证明：矩阵A－2E可逆； (2)若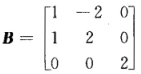
，求矩阵A．
请帮忙给出正确答案和分析，谢谢！
参考解答
463***102
2024-11-16 09:07:08
正确答案：(1)由2A－1B＝B－4E知 AB—2B—4A＝0．从而(A－2E)(B－4E)＝8E或(A－2E).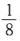
(B－4E)＝E．故A－2E可逆且 (A－2E)－1＝
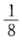(B－4E)． (2)由(1)知A＝2E＋8(B－4E)－1而
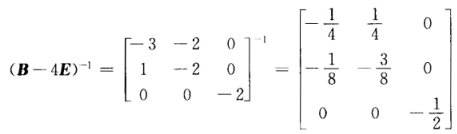故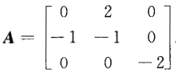
[分析将给定矩阵等式化简整理为(A－2E).C＝E，则可得到(1)的证明．再由(1)得A＝2E＋8(B－4E)－1．[评注在已知一矩阵等式的情况下，讨论某矩阵的可逆性、求逆矩阵或求某个矩阵，一般均应将已知等式化简为逆矩阵的定义形式进行分析．
相似问题
设设α为3维列向量 αT是α的转置。若 则αTα＝_______．设α为3维列向量 αT是α的转置。
设设α为3维列向量，αT是α的转置。若，则αTα＝_______．设α为3维列向量，αT是α的转置。若，则αTα＝_______．请帮忙给出正确答案和分析，谢谢！
通过直线函数u=ln(x2＋y2＋z2)在点M(1 2 一2)处的梯度graduI｜M_____．函
通过直线函数u=ln(x2＋y2＋z2)在点M(1，2，一2)处的梯度graduI｜M_____．函数u=ln(x2+y2+z2)在点M(1，2，一2)处的梯度graduI｜M_____．请帮忙给出正确答案和分析，谢谢！
已知yn＝C1＋C2an是方程yn+2－3yn+1＋2yn＝0的通解 求满足条件的常数a．请帮忙给出
已知yn＝C1＋C2an是方程yn+2－3yn+1＋2yn＝0的通解，求满足条件的常数a．请帮忙给出正确答案和分析，谢谢！
已知ex是方程xyˊ－P(x)y＝x的一个解 求方程满足初值条件y(ln 2)＝0的一个特解．请帮忙
已知ex是方程xyˊ－P(x)y＝x的一个解，求方程满足初值条件y(ln 2)＝0的一个特解．请帮忙给出正确答案和分析，谢谢！
设A是任一n(n≥3)阶方阵 A*是A的伴随矩阵 又k为常数 且k≠0 ±1 则必有(kA)*等于A
设A是任一n(n≥3)阶方阵，A*是A的伴随矩阵，又k为常数，且k≠0，±1，则必有(kA)*等于A．kA*．B．kn－1A*．C．knA*．D．k－1A*．请帮忙给出正确答案和分析，谢谢！
