有一根细棒长为L 质量为m1 且均匀分布．此棒静止地平放在滑动摩擦系数为μ的水平桌面上．它可绕通过其
有一根细棒长为L，质量为m1，且均匀分布．此棒静止地平放在滑动摩擦系数为μ的水平桌面上．它可绕通过其端点O且与桌面垂直的固定光滑轴转动．另有一水平运动的小滑块．质量为m2，以垂直于棒的水平速度v1，从左侧与棒的另一端A碰撞，碰撞时间极短．小滑块在碰撞后的速度为v2，方向与v1相反，如图5-3所示．求细棒在碰撞后开始转动到停止转动的过程中所经历的时间．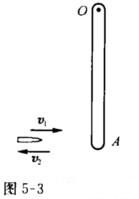 
请帮忙给出正确答案和分析，谢谢！
参考解答
456***100
2024-11-04 00:19:39
正确答案：此题分两个过程：二者的碰撞过程和棒的转动过程． 以棒和滑块为系统由于碰撞时间极短所以棒所受的摩擦力矩远小于滑块与棒之间的冲力矩(内力矩)因此可以认为系统所受的合外力矩为零角动量守恒．设碰撞后棒的角速度为ω则有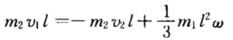
以x表示棒上质元dm离轴O的距离则碰撞后棒在转动过程中所受的摩擦力矩为
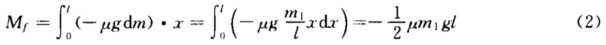冲量距为Mft．由角动量定理可得
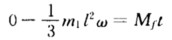联立以上三式求解可得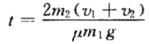
①用角动量守恒定律求解问题时，首先要正确分析角动量守恒的条件是否满足．②角动量守恒是矢量守恒，不仅要注意它的大小，而且还要考虑它的方向．对质点，角动量的方向由L=r×mv来确定；对刚体，角动量的方向由L=Iω来确定．③本题不能应用滑块和棒的总动量守恒来求解．因为滑块撞击棒时．轴对棒有反力．这反力属于外力，因此系统总动量不守恒．
相似问题
一个人站在船上 人与船的总质量为300kg．人用100N的水平力拉一轻绳 绳的另一端系在质量为200
一个人站在船上，人与船的总质量为300kg．人用100N的水平力拉一轻绳，绳的另一端系在质量为200kg的船上．开始时两船都静止，若不计水的阻力，则在开始拉
一个振动系统如图6-3所示。已知二根轻弹簧的劲度系数分别为k1 k2 且k1=k2=1000N.m-
一个振动系统如图6-3所示。已知二根轻弹簧的劲度系数分别为k1、k2，且k1=k2=1000N m-1，木块的质量为M=4 99 kg。一颗质量m=10g的子弹以1000 m s-1的速
在t=0时 周期为T 振幅为A的单摆分别处于图6-9所示(a) (b) (c)三种状态．若选单摆的平
在t=0时，周期为T、振幅为A的单摆分别处于图6-9所示(a)、(b)、(c)三种状态．若选单摆的平衡位置为坐标原点，坐标指向正右方，则单摆作小角度摆动的振动表
一列平面简谐波在弹性介质中传播．在某一瞬时 介质中某质元正处于平衡位置 此时它的能量是( )．A．动
一列平面简谐波在弹性介质中传播．在某一瞬时，介质中某质元正处于平衡位置，此时它的能量是( )．A．动能为零，势能最大B．动能为零，势能为零C．动能最
如图6-7所示 有一个水平弹簧振子 弹簧的劲度系数为24N.m-1 重物的质量为6 kg 重物静止在
如图6-7所示，有一个水平弹簧振子，弹簧的劲度系数为24N m-1，重物的质量为6 kg，重物静止在平衡位置上，设以一个水平恒力F=10 N向左作用于物体（不计
