设α=(a1 a2 … an)T β=(b1 b2 … bn)T都是非零向量 且满足条件αTβ=0

正确答案：(1)由A=αβ^T和α^Tβ=0 有A²=AA=(αβ^T)(αβ^T)=α(β^Tα)β^T=0即A²=0． (2)设A为A的任一特征值A的属于特征值λ的特征向量为x(x≠0)则Ax=λxx≠0于是A²X=λAx=λ²x 因为A²=0所以λ²x=0x≠0故必有λ=0即矩阵A的特征值全为0． 不妨设向量αβ中分量a₁≠0b₁≠0对齐次线性方程组(0E—A)x=0的系数矩阵施以初等行变换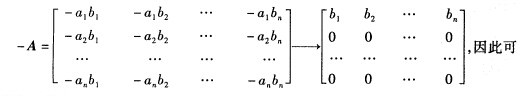．得该方程组的基础解系为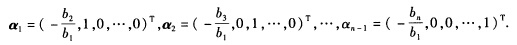于是A的属于特征值λ=0的全部特征向量为 k₁α₁+k₂α₂+…+k_n-1α_n-1(k₁k₂…k_n-1是不全为零的任意常数)．
(1)由A=αβT和αTβ=0,有A2=AA=(αβT)(αβT)=α(βTα)βT=0,即A2=0．(2)设A为A的任一特征值,A的属于特征值λ的特征向量为x(x≠0),则Ax=λx,x≠0,于是A2X=λAx=λ2x,因为A2=0,所以λ2x=0,x≠0,故必有λ=0,即矩阵A的特征值全为0．不妨设向量α,β中分量a1≠0,b1≠0,对齐次线性方程组(0E—A)x=0的系数矩阵施以初等行变换．得该方程组的基础解系为于是,A的属于特征值λ=0的全部特征向量为k1α1+k2α2+…+kn-1αn-1(k1,k2,…,kn-1是不全为零的任意常数)．