设向量α1 α2 … αt是齐次方程组AX=0的一个基础解系 向量β不是方程组AX=0的解 即Aβ≠
设向量α1，α2，…，αt是齐次方程组AX=0的一个基础解系，向量β不是方程组AX=0的解，即Aβ≠0．试证明：向量组β，β+α1，β+α2，…，β+αt，线性无关．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***101
2024-11-11 04:32:54
正确答案：用定义证明．设有一组数kk1k2…kt使得kβ+k1(β+α1)+…+kt(β+αt)=0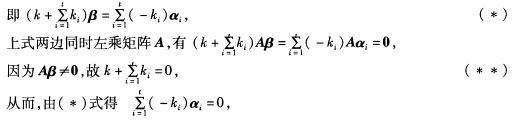
由于向量组α1…αt是基础解系所以 k1=k2=…=kt=0因而由(**)式得k=0．因此向量组ββ+α1…β+αt线性无关．
用定义证明．设有一组数k,k1,k2,…,kt,使得kβ+k1(β+α1)+…+kt(β+αt)=0,由于向量组α1,…,αt是基础解系,所以k1=k2=…=kt=0,因而由(**)式得k=0．因此,向量组β,β+α1,…,β+αt线性无关．
相似问题
设f(x)=2x+3x-2 则当x→0时 f(x)( )．A．与x是同阶但非等价无穷小B．与x是等价
设f(x)=2x+3x-2，则当x→0时，f(x)( )．A．与x是同阶但非等价无穷小B．与x是等价无穷小C．是比x较高阶的无穷小D．是比x较低阶的无穷小请帮忙给出正确答
有机波谱法的灵敏度和准确度比化学分析法高得多。( )此题为判断题(对 错)。请帮忙给出正确答案和分析
有机波谱法的灵敏度和准确度比化学分析法高得多。( )此题为判断题(对，错)。请帮忙给出正确答案和分析，谢谢！
设f(x0)=f(x0)=0 f(x0)＞0 则下列选项正确的是( )．A．f'(x0)是f'(x)
设f(x0)=f(x0)=0，f(x0)＞0，则下列选项正确的是( )．A．f"(x0)是f"(x)的极大值B．f(x0)是f(x)的极大值C．f""(x0)是f(x)的极小值D．点(x0，f(x0))是曲线
已知三阶矩阵A与三维列向量x满足A3x=3Ax—A2x 且向量组x Ax A2x线性无关． (1)记
已知三阶矩阵A与三维列向量x满足A3x=3Ax—A2x，且向量组x，Ax，A2x线性无关． (1)记y=Ax，2=Ay．矩阵P=(x，y，z)，求三阶矩阵B，使AP=PB；(2)求|A|．请
设A为三阶方阵 有3个不同的特征值λ1 λ2 λ3对应的特征向量依次为α1 α2 α3 令β=α1+
设A为三阶方阵，有3个不同的特征值λ1，λ2，λ3对应的特征向量依次为α1，α2，α3，令β=α1+α2+α3，证明：β，Aβ，A2β线性无关．请帮忙给出正确答案和分析，谢谢！
