n级实对称矩阵A是半正定的充分必要条件为A的所有主子式全非负．请帮忙给出正确答案和分析 谢谢！

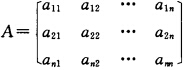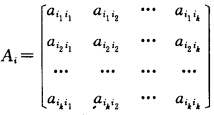正确答案：必要性令则且它们所对应的二次型分别为f(x₁x₂…x_n)；f₁(x_i1x_i2……x_ik)若A是半正定的则是半正定的从而f₁也是半正定的．于是存在实非奇异矩阵C_k使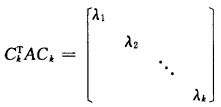其中λ_i≥0(i=12λ…λ)λ为A的特征值．从而｜C_k^TA_kC_k｜=｜A_k｜｜C_k｜²=λ₁λ₂……λ_k≥0又因为｜C_i｜²>0所以A所有主子式全非负．充分性设A的主子式都大于或等于零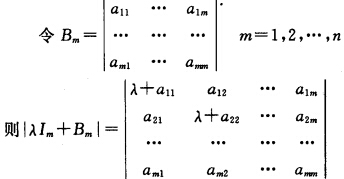=λ^m+p₁λ^m-1+…+p_m-1λ+p_m其中p_i为B_m中的一切i阶主子式之和故p_i≥0故由此可知当λ>0时｜λI_m+B_m｜>0即对任意正实数λλI+A是正定矩阵．假设A不是半正定的则存有X₀=(a₁a₂…a_n)’4=0使X₀^TAX₀=一C<0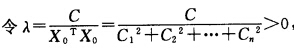则X₀^T(λI+A)X₀=X₀^TλIX₀+X^TAX₀=0这与λ>0时λI+A为正定矩阵相矛盾故A为半正定的．
必要性令则且它们所对应的二次型分别为f(x1,x2,…,xn)；f1(xi1,xi2……xik),若A是半正定的,则,是半正定的,从而f1也是半正定的．于是存在实非奇异矩阵Ck,使其中λi≥0(i=1,2,λ…,λ),λ为A的特征值．从而｜CkTAkCk｜=｜Ak｜｜Ck｜2=λ1,λ2……λk≥0又因为｜Ci｜2>0,所以A所有主子式全非负．充分性设A的主子式都大于或等于零=λm+p1λm-1+…+pm-1λ+pm其中pi为Bm中的一切i阶主子式之和,故pi≥0,故由此可知当λ>0时,｜λIm+Bm｜>0即对任意正实数λ,λI+A是正定矩阵．假设A不是半正定的,则存有X0=(a1,a2,…,an)’4=0,使X0TAX0=一C<0则X0T(λI+A)X0=X0TλIX0+XTAX0=0,这与λ>0时λI+A为正定矩阵相矛盾,故A为半正定的．