求射影变换的逆变换式 并求出影消线 即χ3=0的对应直线的方程.请帮忙给出正确答案和分析 谢谢!
求射影变换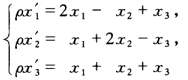 的逆变换式,并求出影消线,即χ3=0的对应直线的方程.
的逆变换式,并求出影消线,即χ3=0的对应直线的方程.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:根据公式(4.4)求出逆变换为: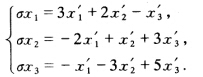 χ1=0的对应直线为:χ′1+3χ′2-5χ′3=0.
χ1=0的对应直线为:χ′1+3χ′2-5χ′3=0.
根据公式(4.4),求出逆变换为:χ1=0的对应直线为:χ′1+3χ′2-5χ′3=0.
相似问题
求下列对合的自对应点的坐标:求使平面7r内四点(1 0 1) (0 1 1) (1 1 1) (0
求下列对合的自对应点的坐标:求使平面7r内四点(1,0,1),(0,1,1),(1,1,1),(0,0,1)分别对应平面π′内求使平面7r内四点(1,0,1),(0,1,1),(
求二圆χ12+χ22-5χ32=0与(χ1-3χ3)2+χ22-8χ32=0的交点.请帮忙给出正确答
求二圆χ12+χ22-5χ32=0与(χ1-3χ3)2+χ22-8χ32=0的交点.请帮忙给出正确答案和分析,谢谢!
设在帕普斯定理里 帕普斯线与直线l1 l2分别交于点P1 P2 l1与l2交于点O 证明:在由三对对
设在帕普斯定理里,帕普斯线与直线l1、l2分别交于点P1、P2,l1与l2交于点O,证明:在由三对对应点A1→A2,B1→B2,C1→C2,所决定的射影对应里O→P2,P1
求对合的方程 这个对合的二重元素的参数为: (1)2与3; (2)方程αt2+2βt+γ的根.请帮忙
求对合的方程,这个对合的二重元素的参数为: (1)2与3; (2)方程αt2+2βt+γ的根.请帮忙给出正确答案和分析,谢谢!
试用作图方法 分别构作双曲型射影变换 抛物型射影变换 椭圆型射影变换.请帮忙给出正确答案和分析 谢谢
试用作图方法,分别构作双曲型射影变换、抛物型射影变换,椭圆型射影变换.请帮忙给出正确答案和分析,谢谢!












