证明：圆柱螺线x(s)=(rcosωs rsinωs cohs)(r h及均为常数)的主法线与它的轴
证明：圆柱螺线x(s)=(rcosωs，rsinωs，cohs)(r，h及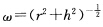
均为常数)的主法线与它的轴(z轴)正交，而从法线与它的轴交于定角．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***102
2024-11-16 22:44:16
正确答案：根据例1．2．3V2(s)=一(cosωssinωs0)V3(s)=ω(hsinωs--hcosωsr)有V2(s).e3=一(cosωssinωs0).(001)=0cosθ=V3(s).e3=ω(hsinωs-hcosωsr).(001)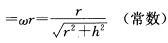
其中θ为V3(s)与e3的夹角．这就表明主法线与z轴正交而从法线与z轴交于定角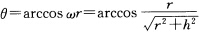
根据例1．2．3,V2(s)=一(cosωs,sinωs,0),V3(s)=ω(hsinωs,--hcosωs,r),有V2(s).e3=一(cosωs,sinωs,0).(0,0,1)=0,cosθ=V3(s).e3=ω(hsinωs,-hcosωs,r).(0,0,1)其中θ为V3(s)与e3的夹角．这就表明主法线与z轴正交,而从法线与z轴交于定角
相似问题
求悬链面M：求旋转曲面M：x(u v)=(f(v)cosu f(v)sinu v)的渐近曲线．求旋转
求悬链面M：求旋转曲面M：x(u，v)=(f(v)cosu，f(v)sinu，v)的渐近曲线．求旋转曲面M：x(u，v)=(f(v)cosu，f(v)sinu，v)的渐近曲线．请帮忙给出正确答案和分析，谢谢！
设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn｜f(x)=0}≠∮ 且对证明：2维单位球
设f(x)为Rn上的一个Cr函数(r≥1)，M={x∈Rn｜f(x)=0}≠∮，且对证明：2维单位球面是可定向的．证明：2维单位球面是可定向的．请帮忙给出正确答案和分析，谢谢！
如果将习题2．9．1中Codazzi方程的L M N分别用E F G代替 则可得到恒等式(猜测)：E
如果将习题2．9．1中Codazzi方程的L，M，N分别用E，F，G代替，则可得到恒等式(猜测)：Ev一Fu=EF121+F(F122一F111)一GF112，Fv一Gu请帮忙给出正确答案和分析，谢谢！
证明：马鞍面M：z=xy为直纹面 但不是可展曲面 其参数表示为x(u v)=(u v uv)．请帮忙
证明：马鞍面M：z=xy为直纹面，但不是可展曲面，其参数表示为x(u，v)=(u，v，uv)．请帮忙给出正确答案和分析，谢谢！
证明：圆柱螺线ρ(v)=(acosv asinv bv) (a>0 b>0)的主法线曲面M是正螺面
证明：圆柱螺线ρ(v)=(acosv，asinv，bv) (a>0， b>0)的主法线曲面M是正螺面x(u，v)=(ucosv，usinv，bv)，它不是可展曲面．请帮忙给出正确答案和分析，谢谢！
