用凑微分法求下列不定积分: 被积函数的分子与分母同乘以一个适当的因式 往往可以使不定积分容易被积函数
用凑微分法求下列不定积分: 被积函数的分子与分母同乘以一个适当的因式,往往可以使不定积分容易
被积函数的分子与分母同乘以一个适当的因式,往往可以使不定积分容易求,用这种方法求下列不定积分: 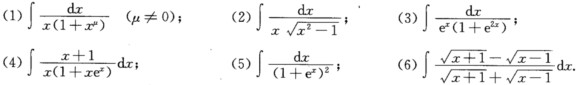
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案: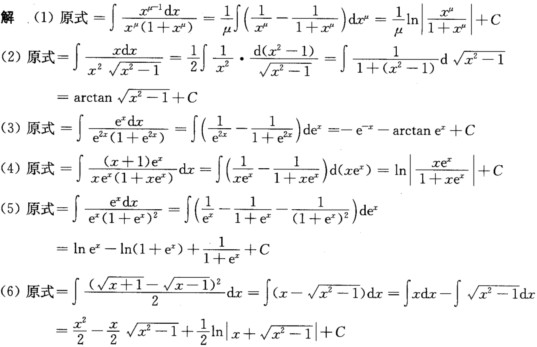
相似问题
设ab>0 f(x)在[a b]上连续 在(a b)内可导 证明:存在ε∈(a b) 使得 设f(x
设ab>0,f(x)在[a,b]上连续,在(a,b)内可导,证明:存在ε∈(a,b),使得 设f(x)在(a,b)内是严格下凸函设f(x)在(a,b)内是严格下凸函数,证明对任何
求下列隐函数的偏导数: 求下列复合函数的偏导数或导数:求下列复合函数的偏导数或导数: 请帮忙给出正确
求下列隐函数的偏导数: 求下列复合函数的偏导数或导数:求下列复合函数的偏导数或导数: 请帮忙给出正确答案和分析,谢谢!
设f(x)=2x+3x一2 则当x→0时( ).A.f(x)是x等价无穷小B.f(x)与x是同阶但非
设f(x)=2x+3x一2,则当x→0时( ).A.f(x)是x等价无穷小B.f(x)与x是同阶但非等价无穷小C.f(x)比x更高阶的无穷小D.f(x)是比x较低阶的无穷小请帮忙给出
设设曲线f(x)=x3+ax与g(x)=bx2+c都通过点(一1 0) 且在点(一1 0)有公切线
设设曲线f(x)=x3+ax与g(x)=bx2+c都通过点(一1,0),且在点(一1,0)有公切线,则a=_____,b=_____,c=__设曲线f(x)=x3+ax与g(x)=bx2+c都通过点(一1,0)
设F(x)=f(-x) 且f(x)有n阶导数 求F(n)(x); (2)设f(x)=xe-x 求f(
设F(x)=f(-x),且f(x)有n阶导数,求F(n)(x); (2)设f(x)=xe-x,求f(n)(x).请帮忙给出正确答案和分析,谢谢!












