如果坐标三点形是由非退化二阶曲线的二切线与切点的连线所构成的 如图1—5—20 求证:曲线方程可写为
如果坐标三点形是由非退化二阶曲线的二切线与切点的连线所构成的,如图1—5—20,求证:曲线方程可写为:C1χ1χ3+C2χ22=0. 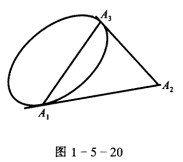
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:设A1A2A3为坐标三点形且A1、A3是切点二阶曲线C的方程为: S≡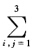 aijχiχj=0 (aij=aji) 因为χ1=0是切线且A3(001)为切点所以SA3=0中必有a23=a33=0χ3≠0又因为χ3=0是切线且A1(100)为切点所以
aijχiχj=0 (aij=aji) 因为χ1=0是切线且A3(001)为切点所以SA3=0中必有a23=a33=0χ3≠0又因为χ3=0是切线且A1(100)为切点所以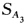 =0中必有a11=a21=0而A2(010)是极线为χ2=0故必有a22≠0. 因此曲线方程可写为a13χ1χ3+a22χ22=0 即C1χ1χ3+C2χ22=0.
=0中必有a11=a21=0而A2(010)是极线为χ2=0故必有a22≠0. 因此曲线方程可写为a13χ1χ3+a22χ22=0 即C1χ1χ3+C2χ22=0.
设A1A2A3为坐标三点形,且A1、A3是切点,二阶曲线C的方程为:S≡aijχiχj=0,(aij=aji)因为χ1=0是切线,且A3(0,0,1)为切点,所以SA3=0中必有a23=a33=0,χ3≠0,又因为χ3=0是切线,且A1(1,0,0)为切点,所以=0中必有a11=a21=0,而A2(0,1,0)是极线为χ2=0,故必有a22≠0.因此曲线方程可写为a13χ1χ3+a22χ22=0,即C1χ1χ3+C2χ22=0.
相似问题
证明:一直线上的射影变换证明:一个变换群的单位元素一定是恒等变换.证明:一个变换群的单位元素一定是恒
证明:一直线上的射影变换证明:一个变换群的单位元素一定是恒等变换.证明:一个变换群的单位元素一定是恒等变换.请帮忙给出正确答案和分析,谢谢!
求证点坐标方程y2=2pχ与线坐标方程pu22-2u1u3=0表示同一曲线.请帮忙给出正确答案和分析
求证点坐标方程y2=2pχ与线坐标方程pu22-2u1u3=0表示同一曲线.请帮忙给出正确答案和分析,谢谢!
证明:一直线上的射影变换的集合构成群 其中△A>0的变换集合也构成群 问△A<0的变换集合是否也构成
证明:一直线上的射影变换的集合构成群,其中△A>0的变换集合也构成群,问△A<0的变换集合是否也构成群?请帮忙给出正确答案和分析,谢谢!
两个射影点列成透视的充要条件是_______.请帮忙给出正确答案和分析 谢谢!
两个射影点列成透视的充要条件是_______.请帮忙给出正确答案和分析,谢谢!
已知二级曲线的三条直线a b c及a b上的切点 试作出二级曲线的另一些直线 并作出c上的切点.请帮
已知二级曲线的三条直线a,b,c及a,b上的切点,试作出二级曲线的另一些直线,并作出c上的切点.请帮忙给出正确答案和分析,谢谢!












