当人们用货币支付各类消费时 这些货币随之流向了另一部分人 这一部分人又从所得收益中提取部分用于自己的
当人们用货币支付各类消费时，这些货币随之流向了另一部分人，这一部分人又从所得收益中提取部分用于自己的各类消费，由此产生了货币的二次流通，货币的这一流通过程可以不停地继续下去，经济学家称之为增值效应．现在假设政府部门最初投入了D元，同时假设处于货币流通过程中的每个人都将其个人收益的100C％用于消费，余下的100S％用于储蓄，这里的C与S分别称为“边际消费倾向”与“边际储蓄倾向”，C与S都是正数，并且C＋S＝1． (1)设sn表示经n次流通后的总消费量，试写出sn的表达式； (2)证明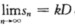
，其中k＝1／S称为增值率； (3)假设边际消费倾向为80％，试问此时k为多少?
请帮忙给出正确答案和分析，谢谢！
参考解答
413***100
2024-11-08 01:21:53
正确答案：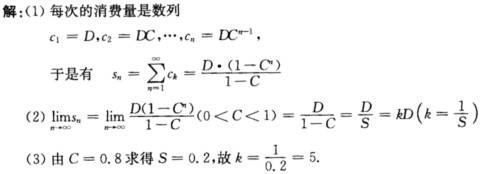
相似问题
把下列函数展开傅里叶级数： (1)f(x)＝sinx／3(－π≤x≤π)； (2)f(x)＝｜sin
把下列函数展开傅里叶级数： (1)f(x)＝sinx／3(－π≤x≤π)； (2)f(x)＝｜sinx｜(－π≤x≤π) (3)f(x)＝cosλx(－π≤x≤π，0＜λ＜1)；(4)请帮忙给出正确答案和分析，谢谢！
证明f(x)＝x－[x]在(－∞ +∞)上是有界周期函数．请帮忙给出正确答案和分析 谢谢！
证明f(x)＝x－[x]在(－∞，+∞)上是有界周期函数．请帮忙给出正确答案和分析，谢谢！
求解下列函数的定义域． 请帮忙给出正确答案和分析 谢谢！
求解下列函数的定义域． 请帮忙给出正确答案和分析，谢谢！
设函数ψ(y)具有连续导数 在围绕原点的任意分段光滑简单闭 请帮忙给出正确答案和分析 谢谢！
设函数ψ(y)具有连续导数，在围绕原点的任意分段光滑简单闭 请帮忙给出正确答案和分析，谢谢！
设函数f(x)在区间(－R R)内可展开成x的幂级数 证明：当f(x)是奇函数时 幂级数中不含x的偶
设函数f(x)在区间(－R，R)内可展开成x的幂级数，证明：当f(x)是奇函数时，幂级数中不含x的偶次幂项；当f(x)是偶函数时，幂级数中不含x的奇次幂项．请帮忙
