设函数f(x)在区间(－R R)内可展开成x的幂级数 证明：当f(x)是奇函数时 幂级数中不含x的偶
设函数f(x)在区间(－R，R)内可展开成x的幂级数，证明：当f(x)是奇函数时，幂级数中不含x的偶次幂项；当f(x)是偶函数时，幂级数中不含x的奇次幂项．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***100
2024-11-08 01:01:21
正确答案：f(x)可在(－RR)内展成x的幂级数因此有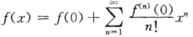
(1)当f(x)为奇函数时由于奇函数的导函数为偶函数偶函数的导函数为奇函数则有f(x)的奇数阶导为偶函数偶数阶导为奇函数当n＝2k时f(n)(x)为奇函数 即f(n)(0)＝0展开式中不含x的偶次项；(2)当f(x)为偶函数时同理有f(x)的奇数阶导为奇函数偶数阶导为偶函数 当n＝2k－1时f(n)(x)为奇函数 即f(n)(0)＝0展开式中不含x的奇次项．
f(x)可在(－R,R)内展成x的幂级数,因此有(1)当f(x)为奇函数时,由于奇函数的导函数为偶函数,偶函数的导函数为奇函数,则有f(x)的奇数阶导为偶函数,偶数阶导为奇函数当n＝2k时,f(n)(x)为奇函数,即f(n)(0)＝0,展开式中不含x的偶次项；(2)当f(x)为偶函数时,同理有f(x)的奇数阶导为奇函数,偶数阶导为偶函数当n＝2k－1时,f(n)(x)为奇函数,即f(n)(0)＝0,展开式中不含x的奇次项．
相似问题
讨论下列级数是否收敛?如果收敛 是条件收敛还是绝对收敛? 请帮忙给出正确答案和分析 谢谢！
讨论下列级数是否收敛?如果收敛，是条件收敛还是绝对收敛? 请帮忙给出正确答案和分析，谢谢！
计算曲面积分 其中S为有向曲面z＝x2＋y2(0≤z≤1)其法向量与z轴正向的夹角为锐角．请帮忙给出
计算曲面积分，其中S为有向曲面z＝x2＋y2(0≤z≤1)其法向量与z轴正向的夹角为锐角．请帮忙给出正确答案和分析，谢谢！
设常数a＞0 则级数( )．A．发散B．绝对收敛C．条件收敛D．收敛性与a的值有关请帮忙给出正确答案
设常数a＞0，则级数( )．A．发散B．绝对收敛C．条件收敛D．收敛性与a的值有关请帮忙给出正确答案和分析，谢谢！
设有一物质曲线Γ 在点(x y z)处它的线密度为μ(x y z) 用第一类曲线积分分别表示： (1
设有一物质曲线Γ，在点(x，y，z)处它的线密度为μ(x，y，z)，用第一类曲线积分分别表示： (1)该物质曲线关于x轴与y轴的转动惯量； (2)该物质曲线对位
用归纳法证明推广的勾股定理：设fi∈R2π(k＝1 2 … n) 且＜fi fj＞＝0 (i≠j；i
用归纳法证明推广的勾股定理：设fi∈R2π(k＝1，2，…，n)，且＜fi，fj＞＝0，(i≠j；i，j＝1，2，…，n)，则 ‖f1＋f2＋…＋fn‖2＝‖f1‖2＋‖f2‖2＋
