用归纳法证明推广的勾股定理：设fi∈R2π(k＝1 2 … n) 且＜fi fj＞＝0 (i≠j；i

正确答案：(1)当n＝2时＜f₁f₂＞＝0←→‖f₁＋f₂‖²＝‖f₁‖²＋‖f₂‖²。(2)假定n＝k时＜f_ifj＞＝0(i≠jij＝12…k)的充要条件为 ‖f_i＋f₂＋…＋f_k‖²＝‖f₁‖²＋‖f₂‖²＋…＋‖f_k‖²。当n＝k＋1时＜f_if_j＞＝0(i≠j；ij＝12…kk＋1)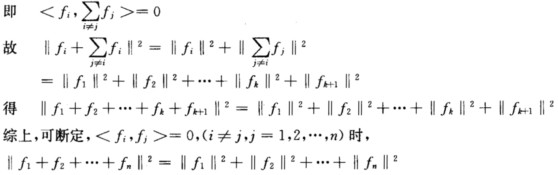
(1)当n＝2时,＜f1,f2＞＝0←→‖f1＋f2‖2＝‖f1‖2＋‖f2‖2。(2)假定n＝k时,＜fi,fj＞＝0(i≠j,ij＝1,2,…k)的充要条件为‖fi＋f2＋…＋fk‖2＝‖f1‖2＋‖f2‖2＋…＋‖fk‖2。当n＝k＋1时,＜fi,fj＞＝0(i≠j；i,j＝1,2,…,k,k＋1)