设总体X～N(μ σ2) X1 X2 … Xn为来自总体X的样本 当用设总体X有概率分布为 作检验H
设总体X～N(μ，σ2)，X1，X2，…，Xn为来自总体X的样本，当用设总体X有概率分布为 作检验H0：θ=0．1，H1：θ=9
设总体X有概率分布为
作检验H0：θ=0．1，H1：θ=9，抽取3个样本，并取拒绝域W为{X1=1，X2=1，X3=1}，试求此时犯第一类错误和第二类错误的概率．
请帮忙给出正确答案和分析，谢谢！
参考解答
413***101
2024-11-12 06:58:38
正确答案：根据定义犯第一类错误的概率α为PH0(W)=Pθ-0.1{X1=1X2=1X3=1)=θ6｜θ6-0.1=0．000001．犯第二类错误的概率β为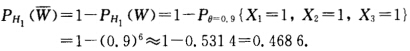 
根据定义犯第一类错误的概率α为PH0(W)=Pθ-0.1{X1=1,X2=1,X3=1)=θ6｜θ6-0.1=0．000001．犯第二类错误的概率β为
相似问题
设某厂生产的灯泡的使用寿命X～N(1 000 σ2)(单位：小时) 随机抽取一容量为9的样本 并测得
设某厂生产的灯泡的使用寿命X～N(1 000，σ2)(单位：小时)，随机抽取一容量为9的样本，并测得了样本均值及样本方差．但是由于工作上的失误，事后失去了
设随机变量X的分布函数为有0～999张奖票 每张奖票售价a元 奖票号若是888 则得头等奖500元
设随机变量X的分布函数为有0～999张奖票，每张奖票售价a元，奖票号若是888，则得头等奖500元，若尾数有0～999张奖票，每张奖票售价a元，奖票号若是888，
设A是n阶实矩阵．证明：存在正交矩阵Q使Q－1AQ为三角矩阵的充要条件是A的特征值全为实数．请帮忙给
设A是n阶实矩阵．证明：存在正交矩阵Q使Q－1AQ为三角矩阵的充要条件是A的特征值全为实数．请帮忙给出正确答案和分析，谢谢！
一袋中装有6只球 编号为1 2 3 4 5 6．在袋中同时取4只球 设X表示取出的4只球中_的最大号
一袋中装有6只球，编号为1，2，3，4，5，6．在袋中同时取4只球，设X表示取出的4只球中_的最大号码，试写出随机变量X的概率分布．请帮忙给出正确答案和分
商店每隔两周进货一次 为了使新的供货到达前商店不会脱销的概率大于0．99 问商店的仓库应至少储存该产
商店每隔两周进货一次，为了使新的供货到达前商店不会脱销的概率大于0．99，问商店的仓库应至少储存该产品多少千克?请帮忙给出正确答案和分析，谢谢！
