设向量组B：b1 b2 … br能由向量组A：a1 a2 … as线性表示为(b1 b2 … br)

正确答案：记A=(a₁a₂…a_s)B=(b₁b₂…b_r)则有B=AK。必要性：设向量组B线性无关知R(B)=r．又由B=AK知R(K)≥R(B)．但K含r列有R(K)≤r于是r=R(B)≤R(K)≤r即R(K)=r．充分性：设R(K)=r．要证B组线性无关．由于Bx=0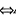Kx=0(因R(A)=s) Lx=0(因R(K)=r) x=0因此向量组B线性无关．
记A=(a1,a2,…,as),B=(b1,b2,…,br),则有B=AK。必要性：设向量组B线性无关,知R(B)=r．又由B=AK,知R(K)≥R(B)．但K含r列,有R(K)≤r,于是r=R(B)≤R(K)≤r,即R(K)=r．充分性：设R(K)=r．要证B组线性无关．由于Bx=0Kx=0(因R(A)=s)Lx=0(因R(K)=r)x=0,因此,向量组B线性无关．