设α=(α1 α2 … αn)T α1≠0 A=ααT (1)证明λ=0是A的n一1重特征值． (

正确答案：(1)因为A=αα^T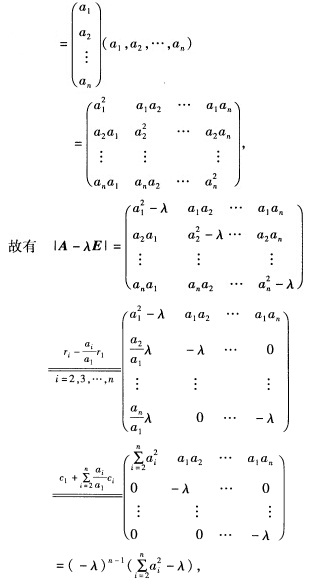所以λ₁=0是A的n—1重特征值另一个特征值是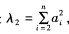由于已知a₁≠0故λ₂非零．(2)由(1)已知求得A的非零特征值为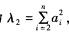这里只要求n个线性无关的特征向量即可．对应特征值λ₁=0解方程(A一0E)x=0由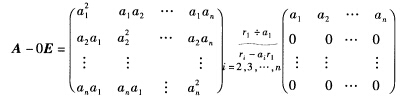得基础解系即线性无关的特征向量为 因为已知A有n个线性无关的特征向量故对应特征值λ₂的特征向量仅有一个即为方程(A—λ₂E)X=0的基础解系仅含一个向量又有因此所要求的n个线性无关的特征向量就是ξ₁ξ₂…ξ_n．
(1)因为A=ααT所以λ1=0是A的n—1重特征值,另一个特征值是由于已知a1≠0,故λ2非零．(2)由(1)已知求得A的非零特征值为这里只要求n个线性无关的特征向量即可．对应特征值λ1=0,解方程(A一0E)x=0,由得基础解系,即线性无关的特征向量为因为已知A有n个线性无关的特征向量,故对应特征值λ2的特征向量仅有一个,即为方程(A—λ2E)X=0的基础解系仅含一个向量,又有因此,所要求的n个线性无关的特征向量就是ξ1,ξ2,…,ξn．