如图5-2所示 一个恒定力矩M作用于斜面顶点的滑轮上．滑轮半径为r 质量为m1 且均匀分布．绕在滑轮
如图5-2所示，一个恒定力矩M作用于斜面顶点的滑轮上．滑轮半径为r，质量为m1，且均匀分布．绕在滑轮上的轻绳一端固定在滑轮边缘上，另一端固定在质量为m2的重物上，重物沿倾角为θ的斜面上升，且与斜面之间的摩擦系数为μ试求：轮子由静止开始转过△θ角后，获得的角速度．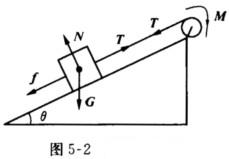 
请帮忙给出正确答案和分析，谢谢！
参考解答
406***100
2024-11-04 03:31:20
正确答案：以重物和滑轮为研究对象承物受力为重力竖直向下支持力垂直斜面向上摩擦力沿斜面向下和绳的张力沿斜面向上；滑轮受力为沿斜面向下的绳的张力和外力矩．重物沿斜面向上运动滑轮做顺时针转动． 对滑轮由转动定律得
对重物由牛顿运动定律得 m2a=T—f—m2gsinθ (2)由摩擦力的定义得 f=μN=μm2gcosθ (3)由线量与角量的关系得 a=ra (4)将式(1)、(2)、(3)和(4)联立求解得到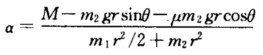
因为角加速度是常量因而可得到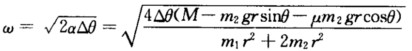
以重物和滑轮为研究对象,承物受力为重力竖直向下,支持力垂直斜面向上,摩擦力沿斜面向下和绳的张力沿斜面向上；滑轮受力为沿斜面向下的绳的张力和外力矩．重物沿斜面向上运动,滑轮做顺时针转动．对滑轮,由转动定律得对重物,由牛顿运动定律得m2a=T—f—m2gsinθ(2)由摩擦力的定义得f=μN=μm2gcosθ(3)由线量与角量的关系得a=ra(4)将式(1)、(2)、(3)和(4)联立求解得到因为角加速度是常量,因而可得到
相似问题
处于保守力场中的某一质点被限制在X轴上运动 它的势能Ep是x的函数 它的总机械能E是一常数 设t=0
处于保守力场中的某一质点被限制在X轴上运动，它的势能Ep是x的函数，它的总机械能E是一常数，设t=0时，质点位于坐标原点，x=0。求证：这一质点从原点运动
一个人从l0m深的井中提水。起始时刻 桶中装有10kg的水 桶的质量为1.0kg。由于水桶漏水 每升
一个人从l0m深的井中提水。起始时刻，桶中装有10kg的水，桶的质量为1 0kg。由于水桶漏水，每升高1 0m要漏去0 20kg的水。求把水桶匀速地从井中提到井口人
一个物体做简谐振动 振动方程为x=Acos(ωt+ 1/4π)．在t=T／4(T为周期)时刻 物体的
一个物体做简谐振动，振动方程为x=Acos(ωt+ 1 4π)．在t=T／4(T为周期)时刻，物体的加速度为( )． A． B． C． D． 请帮忙给出正确答案和分析，谢谢！
一个质点沿X轴做简谐振动 运动学方程为X=4×10-2cos(2πt+ 1/3π)(SI)．从t=0
一个质点沿X轴做简谐振动，运动学方程为X=4×10-2cos(2πt+ 1 3π)(SI)．从t=0时刻起，到质点位置在x=-2cm处，且向x轴正方向运动的最短时间间隔为( )．
巳知飞轮的半径为1.5m 初转速为60/πr.min-1 角加速度为10rad.s-2。试计算在t
巳知飞轮的半径为1 5m，初转速为60 πr min-1，角加速度为10rad s-2。试计算在t = 2s时：（1）飞轮的角速度和角位移；（2）轮缘上点的速度和加速度。请
