将下列函数按勒让德多项式展开： (1)f(x)=x3 (2)f(x)=|x| 设有一个均匀的细圆环

正确答案：取球坐标系坐标原点放在环心而圆环则处在赤道面上这时空间任意一点(rθφ)的引力势应该与φ无关u=u(rθ)可以写出u所满足的方程和部分定解条件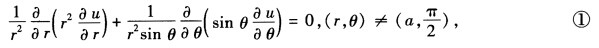： u |_θ=0有界 u |_θ=π有界 u |_r=0有界 u |_r=∞→0要写出均匀细圆环质量分布的体密度势必要用到δ函数方程就变为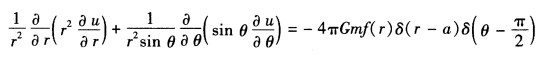其中G是引力函数函数f(r)可以由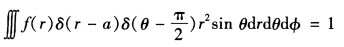定出而且由于f(r)δ(r-a)=f(a)δ(r-a)所以有 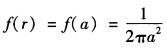由δ函数的性质可以知道当r≠a时方程①就退化为Laplace方程这样再结合有界条件和无穷远条件就得到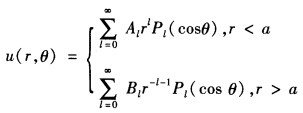然后就应该利用圆环的质量分布(即方程①右端的非齐次项)定出系数A_ι和B_ι。 考虑到δ函数应该是间断函数的导数所以u(rθ)在球面r=a上一定是连续的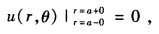а u(rθ)／аr在球面r=a上一定是不连续的它在球面r=a两侧的跃变可以由方程①对r积分得到因此 A_ιa^ι=B_ιa^-ι-1 A_ιla^ι+1+B_ι(ι+1 )a^-ι=(2ι+1)GmP_ι(0)解之即得 A_ι=Gma^-ι-1P_ι(0)B_ι=Gma^ιP_ι(0)所以
取球坐标系,坐标原点放在环心,而圆环则处在赤道面上,这时,空间任意一点(r,θ,φ)的引力势应该与φ无关,u=u(r,θ),可以写出u所满足的方程和部分定解条件：u|θ=0有界,u|θ=π有界,u|r=0有界,u|r=∞→0要写出均匀细圆环质量分布的体密度,势必要用到δ函数,方程就变为其中G是引力函数,函数f(r)可以由定出,而且由于f(r)δ(r-a)=f(a)δ(r-a),所以有由δ函数的性质可以知道,当r≠a时,方程①就退化为Laplace方程,这样,再结合有界条件和无穷远条件,就得到然后就应该利用圆环的质量分布(即方程①右端的非齐次项)定出系数Aι和Bι。考虑到δ函数应该是间断函数的导数,所以u(r,θ)在球面r=a上一定是连续的аu(r,θ)／аr在球面r=a上一定是不连续的,它在球面r=a两侧的跃变可以由方程①对r积分得到因此Aιaι=Bιa-ι-1,Aιlaι+1+Bι(ι+1)a-ι=(2ι+1)GmPι(0)解之即得Aι=Gma-ι-1Pι(0),Bι=GmaιPι(0)所以