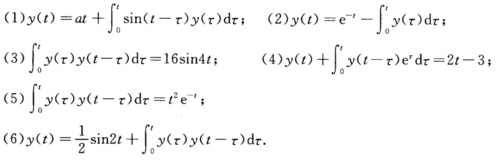参考解答
正确答案:本题中各小题的求解主要利用Laplace变换的卷积定理其他说明均同前两题.并记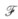 [y(t)=Y(s). (1)原方程可写为y(t)=at+sint*y(t)两边取Laplace变换并利用卷积定理有
[y(t)=Y(s). (1)原方程可写为y(t)=at+sint*y(t)两边取Laplace变换并利用卷积定理有 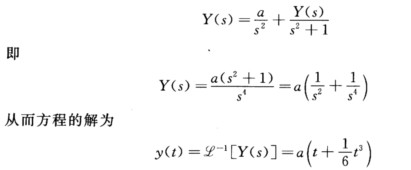 (2)原方程可写为y(t)=e-t一1*y(t)两边取Laplace变换并利用卷积定理.
(2)原方程可写为y(t)=e-t一1*y(t)两边取Laplace变换并利用卷积定理. 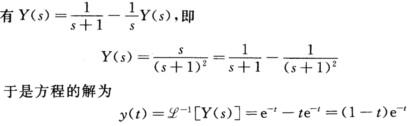 (3)原方程可写为y(t)*y(t)=16sin4t同(1)有
(3)原方程可写为y(t)*y(t)=16sin4t同(1)有  于是方程的解为 y(t)=8J0(4t) 或 y(t)=一8J0(4t) (4)原方程可写为y(t)+y(t)*et=2t一3同(1)有
于是方程的解为 y(t)=8J0(4t) 或 y(t)=一8J0(4t) (4)原方程可写为y(t)+y(t)*et=2t一3同(1)有 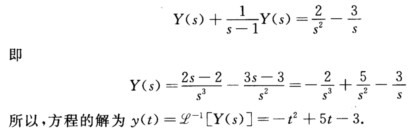 (5)原方程可写为y(t)*y(t)=t2e-t同(1)有
(5)原方程可写为y(t)*y(t)=t2e-t同(1)有  于是方程的解为 y(t)=J1(2t) 或 y(t)=δ(t)一J1(2t)
于是方程的解为 y(t)=J1(2t) 或 y(t)=δ(t)一J1(2t)
本题中各小题的求解,主要利用Laplace变换的卷积定理,其他说明均同前两题.并记[y(t)=Y(s).(1)原方程可写为y(t)=at+sint*y(t),两边取Laplace变换,并利用卷积定理,有(2)原方程可写为,y(t)=e-t一1*y(t),两边取Laplace变换,并利用卷积定理.(3)原方程可写为y(t)*y(t)=16sin4t,同(1),有于是方程的解为y(t)=8J0(4t)或y(t)=一8J0(4t)(4)原方程可写为y(t)+y(t)*et=2t一3,同(1),有(5)原方程可写为y(t)*y(t)=t2e-t,同(1),有于是方程的解为y(t)=J1(2t)或y(t)=δ(t)一J1(2t)
相似问题
求下列函数的Laplace变换式. (1)f(t)=t2+3t+2; (2)f(t)=1一tet;
求下列函数的Laplace变换式. (1)f(t)=t2+3t+2; (2)f(t)=1一tet; (3)f(t)=(t一1)2et; (4)f(t)=sinat; (5)f(t)=tcosat; (6)f(t)=5sin2t一3cos2
设H K是群G的两个子群.证明: 1)(H:H ∩ K)≤(G:K); 2)当(G:K)有限时 则
设H,K是群G的两个子群.证明: 1)(H:H ∩ K)≤(G:K); 2)当(G:K)有限时,则 (H:H∩K)=(G:K)G=HK.请帮忙给出正确答案和分析,谢谢!
利用Laplace变换求下列积分方程的解. 求微分方程组 满足x(0)=0 y(0)=0 z(0)=
利用Laplace变换求下列积分方程的解. 求微分方程组 满足x(0)=0,y(0)=0,z(0)=0的解.求微分方程组 满足x(0)=0,y(0)=0,z(0)=0的解.请帮忙给出正确答案和分析,谢谢!
利用拉盖尔定理求过原点的两直线aχ2+2hχy+by2=0所成的角.请帮忙给出正确答案和分析 谢谢!
利用拉盖尔定理求过原点的两直线aχ2+2hχy+by2=0所成的角.请帮忙给出正确答案和分析,谢谢!
利用卷积定理 证明 请帮忙给出正确答案和分析 谢谢!
利用卷积定理,证明 请帮忙给出正确答案和分析,谢谢!