利用拉盖尔定理求过原点的两直线aχ2＋2hχy＋by2＝0所成的角．请帮忙给出正确答案和分析 谢谢！
利用拉盖尔定理求过原点的两直线aχ2＋2hχy＋by2＝0所成的角．
请帮忙给出正确答案和分析，谢谢！
参考解答
413***102
2024-11-19 08:48:52
正确答案：设相交于O的二直线为l1、l2过O的两条迷向直线是m1、m2∠(l1l2)＝θ由已知： l1：y＝λ1χ其中λ1＝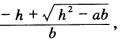
l2：y＝λ2χ其中λ2＝
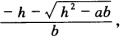λ1.λ2＝
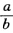λ2λ1＝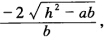
设(l1l2m1m2)＝μ 则
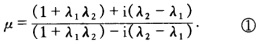由拉盖尔定理
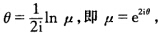由欧拉公式：
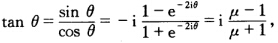又由①得：
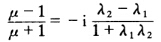所以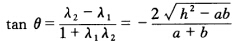
设相交于O的二直线为l1、l2,过O的两条迷向直线是m1、m2,∠(l1,l2)＝θ,由已知：l1：y＝λ1χ,其中λ1＝l2：y＝λ2χ,其中λ2＝λ1.λ2＝,λ2λ1＝设(l1l2,m1m2)＝μ,则由拉盖尔定理由欧拉公式：又由①得：所以
相似问题
利用卷积定理 证明 请帮忙给出正确答案和分析 谢谢！
利用卷积定理，证明 请帮忙给出正确答案和分析，谢谢！
试证：若f(t)满足积分定理的条件 则有 求解积分方程求解积分方程 请帮忙给出正确答案和分析 谢谢！
试证：若f(t)满足积分定理的条件，则有 求解积分方程求解积分方程 请帮忙给出正确答案和分析，谢谢！
设V中的一组基是{e0 e1 … en1} V*的一组基是{e0* e1* … en*} [a b]
设V中的一组基是{e0，e1，…，en1}，V*的一组基是{e0*，e1*，…，en*}，[a，b]是V中一个子空间，求它的零化子空间[a，b]0．请帮忙给出正确答案和分析，谢谢！
求下列二阶超曲面的中心 并指出哪个是抛物面(注意：χ4＝χ0)． (1)aχ12＋bχ22＋cχ32
求下列二阶超曲面的中心，并指出哪个是抛物面(注意：χ4＝χ0)． (1)aχ12＋bχ22＋cχ32－χ42＝0，(abc≠0)； (2)aχ12＋bχ22－2χ3χ4＝0，(ab≠0)
求函数f(t)=δ(t)cost+kektu(t)(k>0)的Laplace变换．请帮忙给出正确答案
求函数f(t)=δ(t)cost+kektu(t)(k>0)的Laplace变换．请帮忙给出正确答案和分析，谢谢！
