求下列二阶超曲面的中心 并指出哪个是抛物面(注意：χ4＝χ0)． (1)aχ12＋bχ22＋cχ32
求下列二阶超曲面的中心，并指出哪个是抛物面(注意：χ4＝χ0)． (1)aχ12＋bχ22＋cχ32－χ42＝0，(abc≠0)； (2)aχ12＋bχ22－2χ3χ4＝0，(ab≠0)； (3)χ22＋χ32－c2χ42＝0，(c≠0)； (4)χ12＋χ22＋χ32＋2χ1χ2＋6χ1χ3－2χ2χ3＋2χ2χ3－6χ2χ4－2χ3χ4＝0．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***102
2024-11-19 08:38:23
正确答案：(1)中心是(0：0：0：1)； (2)抛物面； (3)中心在直线y＝z＝0上它是圆柱面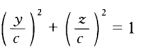
的轴线； (4)
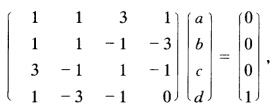所以a：b：C：d＝(－1)：(－1)：1：(－1)． 中心是 (1：1：(－1)：1)．
(1)中心是(0：0：0：1)；(2)抛物面；(3)中心在直线y＝z＝0上,它是圆柱面,的轴线；(4)所以a：b：C：d＝(－1)：(－1)：1：(－1)．中心是(1：1：(－1)：1)．
相似问题
求函数f(t)=δ(t)cost+kektu(t)(k>0)的Laplace变换．请帮忙给出正确答案
求函数f(t)=δ(t)cost+kektu(t)(k>0)的Laplace变换．请帮忙给出正确答案和分析，谢谢！
设M为正整数集 而 τ：1→1 n→n－1(n＞1)； σ：n→n＋1 证明：H={(1) (12)
设M为正整数集，而 τ：1→1，n→n－1(n＞1)； σ：n→n＋1 证明：H={(1)，(12)，(34)，(12)(34)}≤S1．又问：证明：H={(1)，(12)，(34)，(12)(34)}≤
静脉注射时为什么要控制注入溶液的浓度?请帮忙给出正确答案和分析 谢谢！
静脉注射时为什么要控制注入溶液的浓度?请帮忙给出正确答案和分析，谢谢！
证明δ-函数的下列性质： (1)δ-函数是偶函数； 请帮忙给出正确答案和分析 谢谢！
证明δ-函数的下列性质： (1)δ-函数是偶函数； 请帮忙给出正确答案和分析，谢谢！
求直射变换请帮忙给出正确答案和分析 谢谢！
求直射变换请帮忙给出正确答案和分析，谢谢！
