已知直线l1 l3 l4的方程分别为：2χ1＋χ2－χ3＝0 χ1－χ2＋χ3＝0 χ1＝0 且(l

正确答案：如果O是自对应点则 l(P)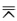l′(P′) 所以P_rP′_r：通过透视中心V(定点)如图2—3—9． 因为VOX是完全四点形P_rP_sP′_sP′_r的对边三点形故有：(ll′OVOX)＝－1 由于直线ll′OV是固定的所以OX是一条固定直线． 如果O不是自对应点设O作为l上的点时O→V′(V′在l′上)O作为l′上的点时U→O如图2—3—10则有(OUP_rP_s)＝(V′OP′_rP′_S)＝(OV′P′_SP′_r)由此得到O点自对应所以(OUP_rP_S)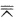(OV′P′_sP′_r)故得三直线UV′P_rP′_sP_sP′_r共点而直线UV′是固定的所以P_rP′_s与P′_rP_s的交点X在固定的直线UV′上．
如果O是自对应点,则l(P)l′(P′)所以PrP′r：通过透视中心V(定点),如图2—3—9．因为VOX是完全四点形PrPsP′sP′r的对边三点形,故有：(ll′,OVOX)＝－1由于直线ll′,OV是固定的,所以OX是一条固定直线．如果O不是自对应点,设O作为l上的点时O→V′(V′在l′上),O作为l′上的点时U→O,如图2—3—10,则有(OU,Pr,Ps)＝(V′O,P′r,P′S,)＝(OV′,P′SP′r,),由此得到O点自对应,所以(O,U,Pr,PS)(O,V′,P′s,P′r),故得三直线UV′,PrP′s,PsP′r共点,而直线UV′是固定的,所以Pr,P′s与P′rPs的交点X在固定的直线UV′上．