R3中k≠0 τ≠0的C4连通曲线x(s)为球面曲线等价于如果x(s)满足:则或者x(s)为球面曲线
R3中k≠0,τ≠0的C4连通曲线x(s)为球面曲线等价于如果x(s)满足:则或者x(s)为球面曲线,或者x(s)为常
如果x(s)满足: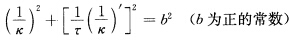 则或者x(s)为球面曲线,或者x(s)为常曲率曲线.
则或者x(s)为球面曲线,或者x(s)为常曲率曲线.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:如果x(s)满足: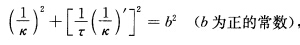 则
则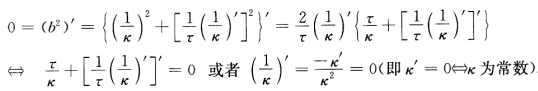 (a)如果对
(a)如果对 有k'(s)≠0则恒有
有k'(s)≠0则恒有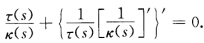 根据习题1.3.22的充分性知x(s)为一条球面曲线.(b)如果{s |k'(s)=0不含区间则对k'(s)≠0的任何s由上述知必有
根据习题1.3.22的充分性知x(s)为一条球面曲线.(b)如果{s |k'(s)=0不含区间则对k'(s)≠0的任何s由上述知必有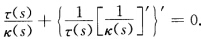 由于{s|k'(s)=0处处稠密且上式左边为s的连续函数所以
由于{s|k'(s)=0处处稠密且上式左边为s的连续函数所以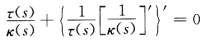 在s的定义区间上恒成立.根据习题1-3.22的充分性知x(s)为一条球面曲线. (c)如果在整个定义区间中k'(s)=0则它等价于x(s)为常数.例如圆柱螺线x(s)=(rcosωsrsinωsωhs)的曲率k(s)=ω2r为常数其中
在s的定义区间上恒成立.根据习题1-3.22的充分性知x(s)为一条球面曲线. (c)如果在整个定义区间中k'(s)=0则它等价于x(s)为常数.例如圆柱螺线x(s)=(rcosωsrsinωsωhs)的曲率k(s)=ω2r为常数其中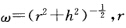 h均为常数.但是它不是球面曲线.
h均为常数.但是它不是球面曲线.
如果x(s)满足:则(a)如果对,有k'(s)≠0,则恒有根据习题1.3.22的充分性知,x(s)为一条球面曲线.(b)如果{s|k'(s)=0不含区间,则对k'(s)≠0的任何s,由上述知,必有由于{s|k'(s)=0处处稠密且上式左边为s的连续函数,所以在s的定义区间上恒成立.根据习题1-3.22的充分性知,x(s)为一条球面曲线.(c)如果在整个定义区间中,k'(s)=0,则它等价于x(s)为常数.例如,圆柱螺线x(s)=(rcosωs,rsinωs,ωhs)的曲率k(s)=ω2r为常数,其中h均为常数.但是,它不是球面曲线.
相似问题
设φ(u v)=常数 φ(u v)=常数为曲面M上的两族正则曲线.证明:两族曲线正交Eφvψv一F(
设φ(u,v)=常数,φ(u,v)=常数为曲面M上的两族正则曲线.证明:两族曲线正交Eφvψv一F(φuψv+φvψu)+Gφuψu=0请帮忙给出正确答案和分析,谢谢!
以下各对函数f(u)与u=g(x)中 哪可以复合构成复合函数f[g(x)]?为什么? 请帮忙给出正确
以下各对函数f(u)与u=g(x)中,哪可以复合构成复合函数f[g(x)]?为什么? 请帮忙给出正确答案和分析,谢谢!
设e1 e2 ω1 ω2和设△1为习题3.2.1中的Laplace算子 即△1f=f11+f33.而
设e1,e2,ω1,ω2和设△1为习题3.2.1中的Laplace算子,即△1f=f11+f33.而△2为[20]1.5节定义5中的Laplac设△1为习题3.2.1中的Laplace算子,即△
证明:负常Gauss(总)曲率曲面证明:常Gauss(总)曲率曲面的第1基本形式可取如下形式:(1)
证明:负常Gauss(总)曲率曲面证明:常Gauss(总)曲率曲面的第1基本形式可取如下形式:(1)当KG=0时,I=证明:常Gauss(总)曲率曲面的第1基本形式可取如下形
证明:半径为R的球面的Gauss(总)曲率为请帮忙给出正确答案和分析 谢谢!
证明:半径为R的球面的Gauss(总)曲率为请帮忙给出正确答案和分析,谢谢!












