证明:负常Gauss(总)曲率曲面证明:常Gauss(总)曲率曲面的第1基本形式可取如下形式:(1)
证明:负常Gauss(总)曲率曲面证明:常Gauss(总)曲率曲面的第1基本形式可取如下形式:(1)当KG=0时,I=
证明:常Gauss(总)曲率曲面的第1基本形式可取如下形式:(1)当KG=0时,I=du2+dv2;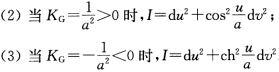
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:取习题2.8.23中的半测地坐标系则第1基本形式为I=du2+G(uv)dv2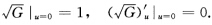 根据Gauss方程:
根据Gauss方程: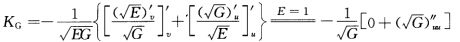
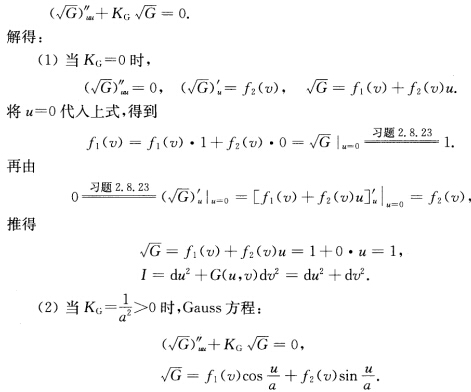 将u=0代入上式得到
将u=0代入上式得到
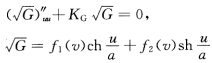 将u=0代入上式得到
将u=0代入上式得到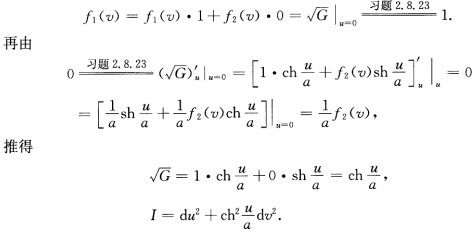
取习题2.8.23中的半测地坐标系,则第1基本形式为I=du2+G(u,v)dv2,根据Gauss方程:将u=0代入上式,得到将u=0代入上式,得到
相似问题
证明:半径为R的球面的Gauss(总)曲率为请帮忙给出正确答案和分析 谢谢!
证明:半径为R的球面的Gauss(总)曲率为请帮忙给出正确答案和分析,谢谢!
R3中一个2维紧致曲面M的洞(窟窿)数称为它的亏格.R3中亏格为g的2维 紧致 定向 连通曲面的Eu
R3中一个2维紧致曲面M的洞(窟窿)数称为它的亏格.R3中亏格为g的2维、紧致、定向、连通曲面的Euler-P0incae示性数X(M)为2(1一g),即X(M)=2(1一g).进而,
设M为R3中的C4正则曲面 x(u1 u2)为其参数表示 P0∈M 且满足:(1)KG(P)>0 即
设M为R3中的C4正则曲面,x(u1,u2)为其参数表示,P0∈M,且满足:(1)KG(P)>0,即P0点的Gauss(总)曲率为正的;(2)在P0点,函数k1达到极大值,同时函数k2达
R3中k≠0 τ≠0的C4连通曲线x(s)为球面曲线等价于证明:具有常曲率k≠0的挠曲线x(s)为B
R3中k≠0,τ≠0的C4连通曲线x(s)为球面曲线等价于证明:具有常曲率k≠0的挠曲线x(s)为Bertrand曲线(s证明:具有常曲率k≠0的挠曲线x(s)为Bertrand曲线(s
我们知道 平面曲线x(t)的曲率中心的轨迹y(t)称为x(t)的渐缩线 x(t)称为y(t)的一条渐
我们知道,平面曲线x(t)的曲率中心的轨迹y(t)称为x(t)的渐缩线,x(t)称为y(t)的一条渐伸线,y(t)的切向量为x(t)的主法向量.试将它推广到空间R3.请帮忙












