求函数y=sin2x一x在试证明对函数y=px2＋qx＋r应用拉格朗日中值定理时所求得的点ξ总是位于
求函数y=sin2x一x在试证明对函数y=px2＋qx＋r应用拉格朗日中值定理时所求得的点ξ总是位于区间的正
试证明对函数y=px2+qx+r应用拉格朗日中值定理时所求得的点ξ总是位于区间的正中间．
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***101
2024-11-12 13:03:18
正确答案：易见本题的多项式函数在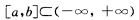
上连续在(ab)内可导即它满足拉格朗日定理的条件故
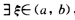使得y'(ξ).(b一a)=f(b)—f(a)而y'(x)一2px+q即有
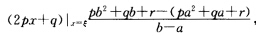亦即2pξ+q=p(b+a)+q所以
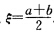证毕．
易见本题的多项式函数在上连续,在(a,b)内可导,即它满足拉格朗日定理的条件,故,使得y'(ξ).(b一a)=f(b)—f(a),而y'(x)一2px+q,即有亦即2pξ+q=p(b+a)+q,所以证毕．
相似问题
一个工人看管三台机床 在一小时内 它们不需要工人照管的概率：第一台是0．9 第二台是0．8 第三台是
一个工人看管三台机床，在一小时内，它们不需要工人照管的概率：第一台是0．9，第二台是0．8，第三台是0．7，且各台机床是否需要工人照管是相互独立的，
设甲 乙两家灯泡厂生产的灯泡的寿命(单位：小时)X和Y的分布律分别为试问哪家工厂生产的灯泡质量较好?
设甲、乙两家灯泡厂生产的灯泡的寿命(单位：小时)X和Y的分布律分别为试问哪家工厂生产的灯泡质量较好?请帮忙给出正确答案和分析，谢谢！
假定f是连续的 而且求下列各值．请帮忙给出正确答案和分析 谢谢！
假定f是连续的，而且求下列各值．请帮忙给出正确答案和分析，谢谢！
验证函数x=C1coskt＋C2sinkt是微分方程求下面微分方程满足所给初始条件的特解：xlnxd
验证函数x=C1coskt＋C2sinkt是微分方程求下面微分方程满足所给初始条件的特解：xlnxdy＋(y一lnx)dx=求下面微分方程满足所给初始条件的特解：xlnxdy+(y一l
求(A—E)-1．请帮忙给出正确答案和分析 谢谢！
求(A—E)-1．请帮忙给出正确答案和分析，谢谢！
