证明二次型f=xTAx在‖x‖=1时的最大值为对称阵A的最大特征值．请帮忙给出正确答案和分析 谢谢！

正确答案：设λ₁≥λ₂≥…≥λ_n为A的n个特征值由对称阵的对角化理论知存在正交阵Q=(q₁q₂…q_n)使 Q^TAQ=diag(λ₁λ₂…λ_n)=A并且Q的第i个列向量q_i是对应于特征值λ_i的单位化特征向量．令正交变换x=Qy则‖x‖²=x^Tx=y^TQ^TQy=y^Ty=‖y‖² ①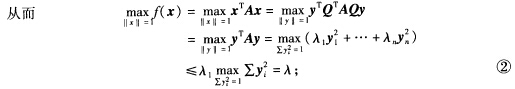 另一方面取y₀=e₁=(10…0)^T即y₀为第1个分量是1的单位坐标向量则‖y₀‖=‖e₁‖=1再取 x₀=Qy ③ 由①式知‖x‖=1且二次型f在x₀的值为 f(x₀)=x₀^TAx=y₀^TQ^TAQy₀=y₀^TAy₀=λ₁ ④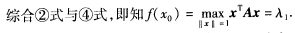
设λ1≥λ2≥…≥λn为A的n个特征值,由对称阵的对角化理论知,存在正交阵Q=(q1,q2,…,qn),使QTAQ=diag(λ1,λ2,…,λn)=A,并且Q的第i个列向量qi是对应于特征值λi的单位化特征向量．令正交变换x=Qy,则‖x‖2=xTx=yTQTQy=yTy=‖y‖2,①另一方面,取y0=e1=(1,0,…,0)T,即y0为第1个分量是1的单位坐标向量,则‖y0‖=‖e1‖=1,再取x0=Qy,③由①式知‖x‖=1,且二次型f在x0的值为f(x0)=x0TAx=y0TQTAQy0=y0TAy0=λ1④