设三阶对称阵A的特征值为λ1=1 λ2=一1 λ3=0；对应λ1 λ2的特征向量依次为求A．请帮忙给
设三阶对称阵A的特征值为λ1=1，λ2=一1，λ3=0；对应λ1，λ2的特征向量依次为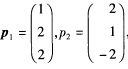
求A．
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***101
2024-11-11 07:59:39
正确答案：因A对称由定理7必有正交阵Q=(q1q2q3)使QTAQ=Q-1AQ=diag(1一10)．显然q1q2可依次取为p1p2的单位化向量即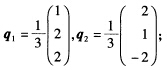
由定理6q3与p1p2正交于是q3可取为方程
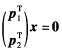的单位解向量．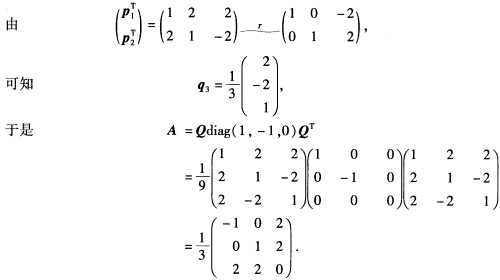
因A对称,由定理7,必有正交阵Q=(q1,q2,q3)使QTAQ=Q-1AQ=diag(1,一1,0)．显然q1,q2可依次取为p1,p2的单位化向量,即由定理6,q3与p1,p2正交,于是q3可取为方程的单位解向量．
相似问题
设有向量组 问α β为何值时 (1)向量b不能由向量组A线性表示． (2)向量b能由向量组A线性
设有向量组 问α，β为何值时， (1)向量b不能由向量组A线性表示． (2)向量b能由向量组A线性表示，且表示式唯一． (3)向量b能由向量组A线性表示，且
设α1 α2 … αm-1(m＞3)线性相关 向量组α2 … αm线性无关 试讨论 (1)α1能否由
设α1，α2，…，αm-1(m＞3)线性相关，向量组α2，…，αm线性无关，试讨论 (1)α1能否由α2，α3，…，αm-1线性表示? (2)αm能否由α1，α2，…，α
试用施密特法把下列向量组正交化： 请帮忙给出正确答案和分析 谢谢！
试用施密特法把下列向量组正交化： 请帮忙给出正确答案和分析，谢谢！
在测试过程必须破坏样品结构的分析方法是( )。A．红外光谱B．核磁共振C．有机质谱D．紫外光谱请帮忙
在测试过程必须破坏样品结构的分析方法是( )。A．红外光谱B．核磁共振C．有机质谱D．紫外光谱请帮忙给出正确答案和分析，谢谢！
应用换元积分法计算不定积分或定积分时 应注意些什么问题?请帮忙给出正确答案和分析 谢谢！
应用换元积分法计算不定积分或定积分时，应注意些什么问题?请帮忙给出正确答案和分析，谢谢！
