设A为n阶实对称矩阵 且A3一3A2+5A一3E=O．证明A正定．请帮忙给出正确答案和分析 谢谢！
设A为n阶实对称矩阵，且A3一3A2+5A一3E=O．证明A正定．
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***101
2024-11-11 05:11:34
正确答案：设λ是A的任一特征值对应特征向量为x≠0即Ax=λx则有 (A2—3A2+5A一3E)x=(λ3一3λ2+5λ一3)x=0亦即λ满足λ3一3λ2+5λ一3=(λ一1)(λ2一2A+3)=0解得λ=1或λ=1±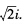
．因A为实对称矩阵其特征值为实数故只有λ=1即A的全部特征值就是λ=1＞0所以A为正定矩阵．
设λ是A的任一特征值,对应特征向量为x≠0,即Ax=λx,则有(A2—3A2+5A一3E)x=(λ3一3λ2+5λ一3)x=0,亦即λ满足λ3一3λ2+5λ一3=(λ一1)(λ2一2A+3)=0,解得λ=1或λ=1±．因A为实对称矩阵,其特征值为实数,故只有λ=1,即A的全部特征值就是λ=1＞0,所以A为正定矩阵．
相似问题
光谱分析法不同于其他分析法主要在于复杂组分的分离与两相分配。( )此题为判断题(对 错)。请帮忙给出
光谱分析法不同于其他分析法主要在于复杂组分的分离与两相分配。( )此题为判断题(对，错)。请帮忙给出正确答案和分析，谢谢！
已知R3的两个基为 求由基a1 a2 a3到基b1 b2 b3的过渡矩阵P．请帮忙给出正确答案和分
已知R3的两个基为 求由基a1，a2，a3到基b1，b2，b3的过渡矩阵P．请帮忙给出正确答案和分析，谢谢！
设λ1 λ2为n阶矩阵A的特征值 且λ1≠λ2 ξ1 ξ2分别是A的属于λ1 λ2的特征向量 证明ξ
设λ1，λ2为n阶矩阵A的特征值，且λ1≠λ2，ξ1，ξ2分别是A的属于λ1，λ2的特征向量，证明ξ1+ξ2不是A的特征向量．请帮忙给出正确答案和分析，谢谢！
光的能量与电磁辐射的( )成正比。A．频率B．波长C．周期D．强度请帮忙给出正确答案和分析 谢谢！
光的能量与电磁辐射的( )成正比。A．频率B．波长C．周期D．强度请帮忙给出正确答案和分析，谢谢！
两个函数相同是什么意思?请帮忙给出正确答案和分析 谢谢！
两个函数相同是什么意思?请帮忙给出正确答案和分析，谢谢！
