对于下述实对称矩阵A 求正交矩阵T 使T-1AT为对角矩阵:请帮忙给出正确答案和分析 谢谢!
对于下述实对称矩阵A,求正交矩阵T,使T-1AT为对角矩阵:
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)显然A为实对称矩阵|λI一A|(λ一1)2(λ+8)=0所以A的特征值为λ1=1(二重)λ2=一8.对λ1=1求得(I一A)X=0的一个基础解系: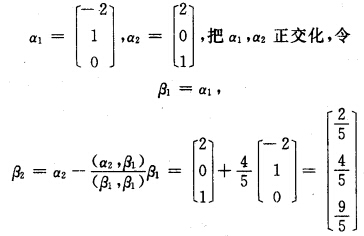 再将β1β2单位化得平
再将β1β2单位化得平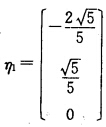
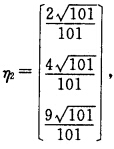 对λ2=一8求得(-8I-A)X=0的一个基础解系为
对λ2=一8求得(-8I-A)X=0的一个基础解系为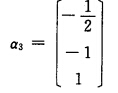 把α3单位化得
把α3单位化得 令
令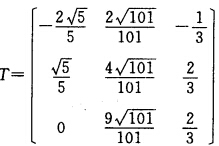 则T是正交矩阵并且有T-1AT=diag{11一8).(2)A为实对称矩阵
则T是正交矩阵并且有T-1AT=diag{11一8).(2)A为实对称矩阵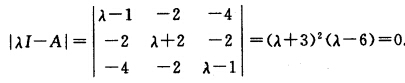 所以A的特征值λ1=一3(二重)λ=6对λ=一3求(一3I一A)X=的一个基础解系得:
所以A的特征值λ1=一3(二重)λ=6对λ=一3求(一3I一A)X=的一个基础解系得: 对λ2=6求(6I一A)X=0的一个基础解系得
对λ2=6求(6I一A)X=0的一个基础解系得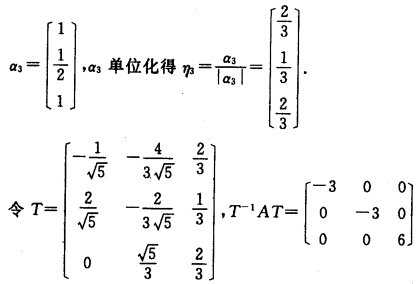 (3)|λI一A|=(λ+1)(λ一2)(λ一5)=0所以A的特征值为λ1=一1=λ2=2λ3=5.对于λ1=一1求得(一I-A)X=0的一个基础解系
(3)|λI一A|=(λ+1)(λ一2)(λ一5)=0所以A的特征值为λ1=一1=λ2=2λ3=5.对于λ1=一1求得(一I-A)X=0的一个基础解系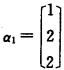 单位化后得
单位化后得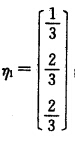 对于λ2=2求得(2I-A)X=0的一个基础解系
对于λ2=2求得(2I-A)X=0的一个基础解系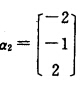 单位化后得
单位化后得 对于λ0=5求得(5I-A)X=0的一个基础解系
对于λ0=5求得(5I-A)X=0的一个基础解系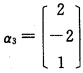 单位化后得
单位化后得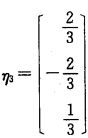 取
取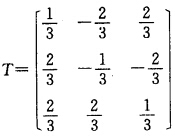 则T为正交矩阵有T-1AT=diag{一125.
则T为正交矩阵有T-1AT=diag{一125.
(1)显然A为实对称矩阵,|λI一A|(λ一1)2(λ+8)=0,所以A的特征值为λ1=1(二重),λ2=一8.对λ1=1求得(I一A)X=0的一个基础解系:再将β1,β2单位化得平对λ2=一8求得(-8I-A)X=0的一个基础解系为把α3单位化得令则T是正交矩阵,并且有T-1AT=diag{1,1,一8).(2)A为实对称矩阵所以A的特征值λ1=一3(二重),λ=6,对λ=一3,求(一3I一A)X=的一个基础解系得:对λ2=6,求(6I一A)X=0的一个基础解系得(3)|λI一A|=(λ+1)(λ一2)(λ一5)=0所以A的特征值为λ1=一1,=λ2=2,λ3=5.对于λ1=一1,求得(一I-A)X=0的一个基础解系单位化后得对于λ2=2,求得(2I-A)X=0的一个基础解系单位化后得对于λ0=5,求得(5I-A)X=0的一个基础解系单位化后得取则T为正交矩阵,有T-1AT=diag{一1,2,5.
相似问题
设求KerA的维数和一个基.求KerA的维数和一个基.请帮忙给出正确答案和分析 谢谢!
设求KerA的维数和一个基.求KerA的维数和一个基.请帮忙给出正确答案和分析,谢谢!
方程组设线性方程组其中Aij为aij在行列式|A|=|aij|中的代数余子式 bi(i=1 2 …
方程组设线性方程组其中Aij为aij在行列式|A|=|aij|中的代数余子式,bi(i=1,2,…,n),ci(i=1,2,…,n)设线性方程组其中Aij为aij在行列式|A|=|
求下列矩阵A的列空间的一个基和行空间的维数:判断下述线性方程组有没有解?有多少解?其中sr≠1.判断
求下列矩阵A的列空间的一个基和行空间的维数:判断下述线性方程组有没有解?有多少解?其中sr≠1.判断下述线性方程组有没有解?有多少解?其中sr≠1.请帮忙
设A是n级矩阵(n≥2) 证明: (1)当n≥3时 (A*)*=|A|n-2A; (2)当n=2时
设A是n级矩阵(n≥2),证明: (1)当n≥3时,(A*)*=|A|n-2A; (2)当n=2时,(A*)*=A请帮忙给出正确答案和分析,谢谢!
证明:数域K上的n级幂零矩阵的特征值都是0.请帮忙给出正确答案和分析 谢谢!
证明:数域K上的n级幂零矩阵的特征值都是0.请帮忙给出正确答案和分析,谢谢!












