求下列矩阵A的列空间的一个基和行空间的维数:判断下述线性方程组有没有解?有多少解?其中sr≠1.判断
求下列矩阵A的列空间的一个基和行空间的维数:判断下述线性方程组有没有解?有多少解?其中sr≠1.
判断下述线性方程组有没有解?有多少解?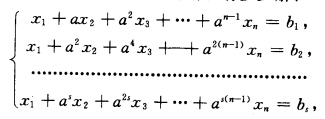 其中sr≠1.
其中sr≠1.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:由于方程的个数小于未知数的个数且0
由于方程的个数小于未知数的个数且0r≠1由此可知方程组必定有解,且有无穷多解.
相似问题
设A是n级矩阵(n≥2) 证明: (1)当n≥3时 (A*)*=|A|n-2A; (2)当n=2时
设A是n级矩阵(n≥2),证明: (1)当n≥3时,(A*)*=|A|n-2A; (2)当n=2时,(A*)*=A请帮忙给出正确答案和分析,谢谢!
证明:数域K上的n级幂零矩阵的特征值都是0.请帮忙给出正确答案和分析 谢谢!
证明:数域K上的n级幂零矩阵的特征值都是0.请帮忙给出正确答案和分析,谢谢!
证明:如果A与B都是n级斜对称矩阵 则AB—BA也是斜对称矩阵.请帮忙给出正确答案和分析 谢谢!
证明:如果A与B都是n级斜对称矩阵,则AB—BA也是斜对称矩阵.请帮忙给出正确答案和分析,谢谢!
如果A2=A 则A叫做幂等矩阵。设A与B都是幂等矩阵 证明A+B是幂等矩阵的充分必要条件是AB=BA
如果A2=A,则A叫做幂等矩阵。设A与B都是幂等矩阵,证明A+B是幂等矩阵的充分必要条件是AB=BA=0.请帮忙给出正确答案和分析,谢谢!
设A是一个n级方阵 且rank(A)=1.证明: (1)A能表示成一个列向量与一个行向量的乘积; (
设A是一个n级方阵,且rank(A)=1.证明: (1)A能表示成一个列向量与一个行向量的乘积; (2)A2=kA,其中k是某个数.请帮忙给出正确答案和分析,谢谢!












