假设某消费者的效用函数为U(x1 x2)=lnx1+x2。试证明：给定商品1和2的价格p1和p2。如
假设某消费者的效用函数为U(x1，x2)=lnx1+x2。试证明：给定商品1和2的价格p1和p2。如果消费者的收入I足够高。则收入的变化不会影响该消费者对商品1的消费。(电子科技大学2009研)
请帮忙给出正确答案和分析，谢谢！
参考解答
4j7***773
2024-06-10 21:44:27
正确答案：该消费者的效用最大化行为可表示为：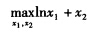
s．t．p1x1+p2x2=I 构造拉格朗日辅助函数L=lnx1+x2一λ(p1x1+p2x2一I)。拉格朗日定理认为最优选择必定满足以下三个一阶条件：
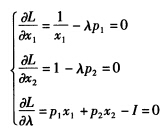求解得效用最大化时消费者对商品1的需求为
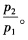所以如果消费者的收入I足够高则收入的变化不会导致该消费者对商品1消费的变化即对商品1的需求不受收入影响。
该消费者的效用最大化行为可表示为：s．t．p1x1+p2x2=I构造拉格朗日辅助函数L=lnx1+x2一λ(p1x1+p2x2一I)。拉格朗日定理认为,最优选择必定满足以下三个一阶条件：求解得效用最大化时消费者对商品1的需求为所以,如果消费者的收入I足够高,则收入的变化不会导致该消费者对商品1消费的变化,即对商品1的需求不受收入影响。
相似问题
边际报酬递减规律(厦门大学2006研)请帮忙给出正确答案和分析 谢谢！
边际报酬递减规律(厦门大学2006研)请帮忙给出正确答案和分析，谢谢！
从x＞y和y＞z推导x＞z。(提示：请从偏好关系的定义出发解题)(中山大学2004研)请帮忙给出正确
从x＞y和y＞z推导x＞z。(提示：请从偏好关系的定义出发解题)(中山大学2004研)请帮忙给出正确答案和分析，谢谢！
某产品市场只有两个生产同质产品的寡头厂商1和2。他们面临的市场需求函数为Q=4000—10P．他们的
某产品市场只有两个生产同质产品的寡头厂商1和2。他们面临的市场需求函数为Q=4000—10P．他们的成本函数分别为：TC1=0．1Q12+20Q1+100000和TC2=0．4Q22+3
亨利消费啤酒(B)和咖啡(C) 开始时 他的预算约束线可以表示为B=20一2C；后来他的预算线变成B
亨利消费啤酒(B)和咖啡(C)，开始时，他的预算约束线可以表示为B=20一2C；后来他的预算线变成B=10—C。预算线的变化可以被下面哪种情形所解释?( )(上海财
规模报酬递增是在下述哪一种情况下发生的?( )。(中山大学2006研)A．按比例连续增加各种生产要素
规模报酬递增是在下述哪一种情况下发生的?( )。(中山大学2006研)A．按比例连续增加各种生产要素B．不按比例连续增加各种生产要素C．连续投入某种生产要
