设随机变量(X Y)的分布函数为 F(x y)=A(arctan ex)(arctan ey) 求:
设随机变量(X,Y)的分布函数为 F(x,y)=A(arctan ex)(arctan ey),求:(1)常数A;(2)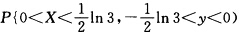 ;(3)关于X和关于Y的边缘分布函数,问X与Y是否独立?(4)(X,Y)的概率密度.
;(3)关于X和关于Y的边缘分布函数,问X与Y是否独立?(4)(X,Y)的概率密度.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)由二维分布函数的性质(2)有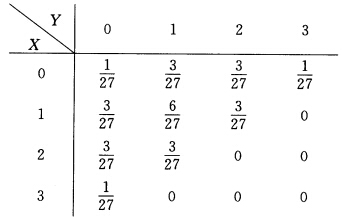 容易看到对一切xy有F(xy)=Fx(x)Fy(y)可见X与Y独立. (4)由二维概率密度的性质(3)有
容易看到对一切xy有F(xy)=Fx(x)Fy(y)可见X与Y独立. (4)由二维概率密度的性质(3)有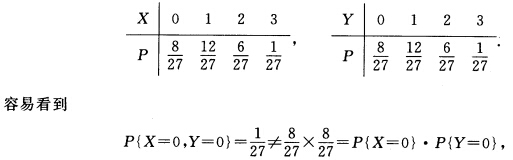
(1)由二维分布函数的性质(2),有容易看到,对一切x,y有F(x,y)=Fx(x)Fy(y),可见X与Y独立.(4)由二维概率密度的性质(3),有
相似问题
设二维随机变量(X Y)的概率密度为 求:①常数A;②P{X+Y<1);③P{X< y<1);④P
设二维随机变量(X,Y)的概率密度为 求:①常数A;②P{X+Y<1);③P{X<,y<1);④P{x>y}.请帮忙给出正确答案和分析,谢谢!
设二维离散型随机变量(X Y)的分布律为 m=0 1 2 … K n=0 1 … m 0<p<
设二维离散型随机变量(X,Y)的分布律为 , m=0,1,2,…,K,n=0,1,…,m, 0<p<1,q=1一p, 其中K为已知正整数,求关于X和关于Y的边缘分布律,
设二维连续型随机变量(X Y)的概率密度为 求关于X和关于Y的边缘概率密度.问X与Y是否独立?请帮
设二维连续型随机变量(X,Y)的概率密度为 求关于X和关于Y的边缘概率密度.问X与Y是否独立?请帮忙给出正确答案和分析,谢谢!
设二维随机变量(X1 X2)~N(1 1 22 22 ) Y1=X1+X2 Y2=X1一2X2 求(
设二维随机变量(X1,X2)~N(1,1,22,22,),Y1=X1+X2,Y2=X1一2X2,求(Y1,Y2)的分布.请帮忙给出正确答案和分析,谢谢!
设离散型随机变量X服从超几何分布 其分布律为 P{X=k)= k=0 1 … l 其中N>0 M>
设离散型随机变量X服从超几何分布,其分布律为 P{X=k)=,k=0,1,…,l, 其中N>0,M>0,n≤N—M,l=min{M,n}.求E(X)和D(X).请帮忙给出正确答案和分析,谢谢!












