设二维连续型随机变量的概率密度为 求:(1)常数A; (2)P{X+Y≤1} P{1<X<2 0<
设二维连续型随机变量的概率密度为 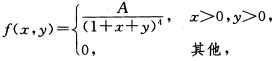 求:(1)常数A; (2)P{X+Y≤1},P{1<X<2,0<Y<1); (3)(X,y)的分布函数.
求:(1)常数A; (2)P{X+Y≤1},P{1<X<2,0<Y<1); (3)(X,y)的分布函数.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)由概率密度的性质(2)应有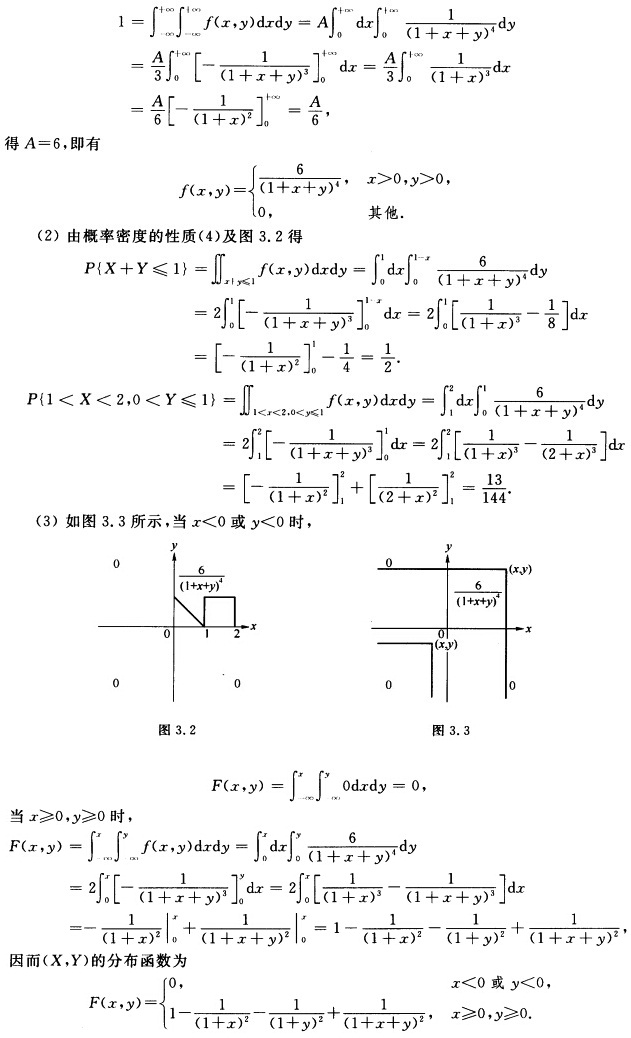
(1)由概率密度的性质(2),应有
相似问题
设随机变量X~π(λ) 求E[|X—E(X)|].请帮忙给出正确答案和分析 谢谢!
设随机变量X~π(λ),求E[|X—E(X)|].请帮忙给出正确答案和分析,谢谢!
设随机变量(X Y Z)的概率密度为 求(X Y Z)的协方差矩阵.请帮忙给出正确答案和分析 谢谢
设随机变量(X,Y,Z)的概率密度为 求(X,Y,Z)的协方差矩阵.请帮忙给出正确答案和分析,谢谢!
设三维随机变量(X Y Z)的协方差矩阵为 若U=2X+3Y+Z V=X一2Y+5Z W=Y—Z
设三维随机变量(X,Y,Z)的协方差矩阵为 若U=2X+3Y+Z,V=X一2Y+5Z,W=Y—Z,求(U,V,W)的协方差矩阵.请帮忙给出正确答案和分析,谢谢!
设X~N(0 σ2) 求E(Xn) n=1 2 ….请帮忙给出正确答案和分析 谢谢!
设X~N(0,σ2),求E(Xn),n=1,2,….请帮忙给出正确答案和分析,谢谢!
设二维随机变量(X Y)满足: E(X)=E(Y)=0 D(X)=D(Y)=1 Cov(X Y)=c
设二维随机变量(X,Y)满足: E(X)=E(Y)=0,D(X)=D(Y)=1,Cov(X,Y)=c, 证明: 请帮忙给出正确答案和分析,谢谢!












