一个水平转台可绕铅直轴自由转动 其半径为r=3m 转动惯量I=450kg.m2 开始时处于静止状态。
一个水平转台可绕铅直轴自由转动,其半径为r=3m,转动惯量I=450kg.m2,开始时处于静止状态。一个质量为m=50 kg的人从转台中心走到转台边缘并沿边缘相对于转台以v=1m.s-1的速度行走。求转台的角速度。
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:对人和转台组成的系统在人走动时系统所受的对垂直轴的合外力矩为零所以系统对此轴的角动量守恒。以j和I分别表示人和转台对轴的转动惯量并以ω和Ω分别表示任一时刻人和转台绕轴的角速度。由于起始角动量为零角动量守恒给出jω+IΩ=0 (1)其中j=mr2。由速度变换式可知V=ωr-Ωr (2)将式(1)和(2)联立求解并将数据m=50kgr=3mv=1m.s-1I=450kg.m2代入可得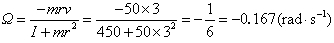
对人和转台组成的系统,在人走动时系统所受的对垂直轴的合外力矩为零,所以系统对此轴的角动量守恒。以j和I分别表示人和转台对轴的转动惯量,并以ω和Ω分别表示任一时刻人和转台绕轴的角速度。由于起始角动量为零,角动量守恒给出jω+IΩ=0(1)其中j=mr2。由速度变换式可知V=ωr-Ωr(2)将式(1)和(2)联立求解,并将数据m=50kg,r=3m,v=1m.s-1,I=450kg.m2代入,可得
相似问题
一块圆板绕垂直于板面的水平对称轴以ω1=25rad.s-1的角速度自转 而该水平轴又以ω2 = 5
一块圆板绕垂直于板面的水平对称轴以ω1=25rad s-1的角速度自转,而该水平轴又以ω2 = 5 rad s-1的角速度绕铅直轴转动。求圆板的角速度。请帮忙给出正
一个质量为M 半径为R并以角速度ω转动着的飞轮(可看作匀质圆盘).在某一瞬时突然有一片质量为m的碎片
一个质量为M、半径为R并以角速度ω转动着的飞轮(可看作匀质圆盘).在某一瞬时突然有一片质量为m的碎片从轮的边缘上飞出,如图5-4所示.假定碎片脱离飞轮
一个做简谐振动的物体 质量为0.20kg 振幅为2.0cm 最大加速度为4.0 cm.s-2。(1)
一个做简谐振动的物体,质量为0 20kg,振幅为2 0cm,最大加速度为4 0 cm s-2。(1)求振动的机械能;(2)物体在什么位置时动能和势能相等?(3)当物体
一个匀质圆盘由静止开始以恒定角加速度绕通过中心且垂直于盘面的轴转动.在某一时刻转速为10r·s-1
一个匀质圆盘由静止开始以恒定角加速度绕通过中心且垂直于盘面的轴转动.在某一时刻转速为10r·s-1,转过60圈后转速变为15r·s-1.则由静止转到10r·s-1
两个皮带轮的半径各为R1和R2 重量各为P1和P2 两轮以皮带相连结 可绕两平行的固定轴转动 如图5
两个皮带轮的半径各为R1和R2,重量各为P1和P2,两轮以皮带相连结,可绕两平行的固定轴转动,如图5-9所示。今在第一个皮带轮上作用一力矩M,试求两轮的角












