一个质量为M 半径为R并以角速度ω转动着的飞轮(可看作匀质圆盘)．在某一瞬时突然有一片质量为m的碎片

正确答案：(1)碎片离盘瞬时线速度即是它上升的初速度 v₀=R_ω (1)设碎片上升高度h时的速度为v则有 v²=v₀²—2gh (2)令v=0可求出上升最大高度为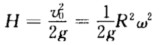 (2)圆盘的转动惯量I=MR²／2．碎片抛出后阋盘的转动惯最I'=MR²／2—mR²．碎片脱离前盘的角动量为Iw；碎片刚脱离后碎片与破盘之间的内力变为零．内力不影响系统的总角动量碎片与破盘的总角动量守恒即 Iω=I'ω'+mv₀R (3)式中ω'为破盘的角速度．将转动惯量代入式(3)有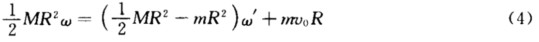式(1)和(4)联立求解得 ω'=ω (角速度不变)圆盘余下部分的角动量为 (1/2 MR²—mR²)ω转动动能为E_k=1/2(1/2 MR²—mR²)ω²
(1)碎片离盘瞬时线速度即是它上升的初速度v0=Rω(1)设碎片上升高度h时的速度为v,则有v2=v02—2gh(2)令v=0,可求出上升最大高度为(2)圆盘的转动惯量I=MR2／2．碎片抛出后,阋盘的转动惯最I'=MR2／2—mR2．碎片脱离前,盘的角动量为Iw；碎片刚脱离后,碎片与破盘之间的内力变为零．内力不影响系统的总角动量,碎片与破盘的总角动量守恒,即Iω=I'ω'+mv0R(3)式中ω'为破盘的角速度．将转动惯量代入式(3)有式(1)和(4)联立求解得ω'=ω(角速度不变)圆盘余下部分的角动量为(1/2MR2—mR2)ω转动动能为Ek=1/2(1/2MR2—mR2)ω2