一个内半径为R1 外半径为R2的厚球壳均匀带电 体电荷密度为ρ。求球壳内 外电场强度的分布。请帮忙给

正确答案：由球壳带电的球对称性可知电场分布也具有球对称性。即到球心距离为r的球面上电场强度大小处处相等方向处处垂直球面（沿半径方向）。于是以任意长r为半径做一个同心球面为高斯面。则通过该高斯面的电通量为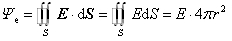（1）当场点在球壳外（r>R₂）时高斯面内包围的电荷为整个球壳带的电荷即ρv=ρ.4π(R₂³-R₁³)/3。由高斯定理和式（1）可得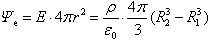（2）求解式（2）得到球壳外场点的电场强度为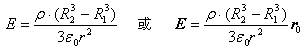当场点P在球壳里（R₁＜r＜R₂）时高斯面包围的电量为ρv=ρ.4π(r³-R₁³)/3。由高斯定理和式（1）可得 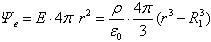（3）求解式（3）得到球壳里场点的电场强度为 当场点P在球壳内（r＜R₁）时高斯面包围的电量为0。由高斯定理和式（1）可得ψ_e=E.4πr²=0 （4）求解式（4）得到球壳内场点的电场强度为 E=0综上可得均匀带电厚球壳内、外的电场强度为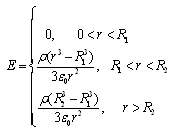
由球壳带电的球对称性可知,电场分布也具有球对称性。即到球心距离为r的球面上电场强度大小处处相等,方向处处垂直球面（沿半径方向）。于是以任意长r为半径做一个同心球面为高斯面。则通过该高斯面的电通量为（1）当场点在球壳外（r>R2）时,高斯面内包围的电荷为整个球壳带的电荷,即ρv=ρ.4π(R23-R13)/3。由高斯定理和式（1）可得（2）求解式（2）得到球壳外场点的电场强度为当场点P在球壳里（R1＜r＜R2）时,高斯面包围的电量为ρv=ρ.4π(r3-R13)/3。由高斯定理和式（1）可得（3）求解式（3）得到球壳里场点的电场强度为当场点P在球壳内（r＜R1）时,高斯面包围的电量为0。由高斯定理和式（1）可得ψe=E.4πr2=0（4）求解式（4）得到球壳内场点的电场强度为E=0综上可得,均匀带电厚球壳内、外的电场强度为