试证非对合的射影变换一定可分解成两个对合之积 并将如下射影变换φ分解成两个对合之积: 请帮忙给出正确
试证非对合的射影变换一定可分解成两个对合之积,并将如下射影变换φ分解成两个对合之积: 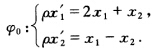
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:设φ是非对合的射影变换取一点A有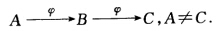 作射影变换φ1使
作射影变换φ1使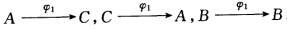 则φ1是对合. 作射影变换φ2使φ2=φ.φ1则有 φ2(B)=φ.φ1(B)=φ(B)=C φ2(C)=φ.φ1(C)=φ(A)=B所以φ2是对合又 φ2.φ1=(φ.φ1).φ1=φ.φ12=φ 所以φ可分解为两个对合变换φ2与φ1之积. 对于已知变换
则φ1是对合. 作射影变换φ2使φ2=φ.φ1则有 φ2(B)=φ.φ1(B)=φ(B)=C φ2(C)=φ.φ1(C)=φ(A)=B所以φ2是对合又 φ2.φ1=(φ.φ1).φ1=φ.φ12=φ 所以φ可分解为两个对合变换φ2与φ1之积. 对于已知变换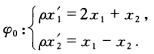 取点(01)则点(01)
取点(01)则点(01)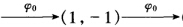 (12)作对合φ1使(01)→(12)→(01)(1-1)→(1-1) 则有
(12)作对合φ1使(01)→(12)→(01)(1-1)→(1-1) 则有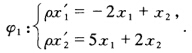 作φ2使φ2=φ0.φ1则有
作φ2使φ2=φ0.φ1则有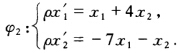 所以φ0=φ2.φ1其中φ1φ2是对合.
所以φ0=φ2.φ1其中φ1φ2是对合.
设φ是非对合的射影变换,取一点A,有作射影变换φ1,使,则φ1是对合.作射影变换φ2,使φ2=φ.φ1,则有φ2(B)=φ.φ1(B)=φ(B)=C,φ2(C)=φ.φ1(C)=φ(A)=B,所以φ2是对合,又φ2.φ1=(φ.φ1).φ1=φ.φ12=φ所以φ可分解为两个对合变换φ2与φ1,之积.对于已知变换取点(0,1),则点(0,1)(1,2),作对合φ1,使(0,1)→(1,2)→(0,1),(1,-1)→(1,-1),则有作φ2,使φ2=φ0.φ1,则有所以φ0=φ2.φ1,其中φ1,φ2是对合.
相似问题
已知共点直线l1 l2 l4的方程为:l1:2χ-y+1=0.l2:3χ+y-2=0 l4:5χ-1
已知共点直线l1,l2,l4的方程为:l1:2χ-y+1=0.l2:3χ+y-2=0,l4:5χ-1=0,且(l1l2,l3l4)=,求l3的方程.请帮忙给出正确答案和分析,谢谢!
求下列对合的自对应点的坐标:求射影变换:的不变元素.求射影变换:的不变元素.请帮忙给出正确答案和分析
求下列对合的自对应点的坐标:求射影变换:的不变元素.求射影变换:的不变元素.请帮忙给出正确答案和分析,谢谢!
设直线l上的点P1(0) P2(1) P3(2)经过射影对应顺次对应l′上的点P′1(一1) P′2
设直线l上的点P1(0),P2(1),P3(2)经过射影对应顺次对应l′上的点P′1(一1),P′2(O),P′3(-2),求射影对应式,并化为齐次坐标式,求出l及l′上的无穷
已知直线l1 l3 l4的方程分别为:2χ1+χ2-χ3=0 χ1-χ2+χ3=0 χ1=0 且(l
已知直线l1,l3,l4的方程分别为:2χ1+χ2-χ3=0,χ1-χ2+χ3=0,χ1=0,且(l1l2,l3l4)=-,求l2的方程.请帮忙给出正确答案和分析,谢谢!
用代数法证明平面上德萨格定理的逆定理. 德萨格定理的逆定理:设三点形A1B1C1与A2B2C2在同一
用代数法证明平面上德萨格定理的逆定理. 德萨格定理的逆定理:设三点形A1B1C1与A2B2C2在同一平面内,B1C1与B2C2的交点为X,C1A1与C2A2的交点为y,A1B1












