用代数法证明平面上德萨格定理的逆定理． 德萨格定理的逆定理：设三点形A1B1C1与A2B2C2在同一

正确答案：如图1—2—16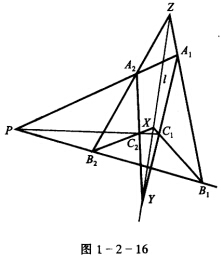．令三点形A₁B₁C₁与A₂B₂C₂的边B₁C₁C₁A₁A₁B₁与B₂C₂C₂A₂A₂B₂的齐次方程顺次为： α₁＝0β₁＝0γ₁＝0 与α₂＝0β₂＝0γ₂＝0又直线l的方程为δ＝0． 因为B₁C₁B₂C₂l相交于一点X根据定理3．4l的方程可用B₁C₁和B₂C₂的方程线性表示即存在二非零常数P₁P₂使 δ≡P₁α₁－p₂α₂． 同理：δ≡q₁β₁－q₂β₂ δ≡r₁γ₁－r₂γ₂ 其中q₁q₂r₁r₂是非零常数因此 P₁α₁－P₂α₂≡q₁β₁－q₂β₂≡r₁γ₁－r₂γ₂． 由此推出： q₁β₁－r₁γ₁≡q₂β₂－r₂γ₂ r₁γ₁－p₁α₁≡r₂γ₂－p₂α₂ P₁α₁－q₁β₁≡p₂α₂－q₂β₂． 由上式推出：q₁β₁－r₁γ₁＝0与q₂β₂－r₂γ₂＝0表示同一直线但q₁β₁－r₁γ₁＝0表示通过二直线β₁＝0与γ₁＝0交点A₁的直线q₂β₂－r₂γ₂＝0表示通过β₂＝0与γ₂＝0的交点A：的直线所以q₁β₁－r₁γ₁＝0与q₂β₂－r₂γ₂＝0均表示直线A₁A₂． 同理可求得直线B₁B₂、C₁C₂的方程． 因此有：A₁A₂：q₁β₁－r₁γ₁＝0或q₂β₂－r₂γ₂＝0． B₁B₂：r₁γ₁－p₁α₁＝0或r₂γ₂－pα＝0． C₁C₂：p₁α₁－q₁β₁＝0或p₂α₂－q₂β₂＝0． 由于1.(q₁β₁－r₁γ₁)＋1.(r₁γ₁－p₁α₁)＋1.(p₁α₁－q₁β₁)＝0 所以三直线A₁A₂B₁B₂C₁C₂交于一点德萨格定理的逆定理得证．
如图1—2—16．令三点形A1B1C1与A2B2C2的边B1C1,C1A1,A1B1与B2C2,C2A2,A2B2的齐次方程顺次为：α1＝0,β1＝0,γ1＝0与α2＝0,β2＝0,γ2＝0,又直线l的方程为δ＝0．因为B1C1,B2C2,l相交于一点X,根据定理3．4,l的方程可用B1C1和B2C2的方程线性表示,即存在二非零常数P1,P2使δ≡P1α1－p2α2．同理：δ≡q1β1－q2β2,δ≡r1γ1－r2γ2,其中q1,q2,r1,r2是非零常数,因此P1α1－P2α2≡q1β1－q2β2≡r1γ1－r2γ2．由此推出：q1β1－r1γ1≡q2β2－r2γ2,r1γ1－p1α1≡r2γ2－p2α2,P1α1－q1β1≡p2α2－q2β2．由上式推出：q1β1－r1γ1＝0与q2β2－r2γ2＝0表示同一直线,但q1β1－r1γ1＝0表示通过二直线β1＝0与γ1＝0交点A1的直线,q2β2－r2γ2＝0表示通过β2＝0与γ2＝0的交点A：的直线,所以q1β1－r1γ1＝0与q2β2－r2γ2＝0均表示直线A1A2．同理可求得直线B1B2、C1C2的方程．因此有：A1A2：q1β1－r1γ1＝0或q2β2－r2γ2＝0．B1B2：r1γ1－p1α1＝0或r2γ2－pα＝0．C1C2：p1α1－q1β1＝0或p2α2－q2β2＝0．由于1.(q1β1－r1γ1)＋1.(r1γ1－p1α1)＋1.(p1α1－q1β1)＝0,所以三直线A1A2,B1B2,C1C2交于一点,德萨格定理的逆定理得证．