设A B均为n阶矩阵 若E-AB可逆 证明E-BA可逆．请帮忙给出正确答案和分析 谢谢！
设A，B均为n阶矩阵，若E-AB可逆，证明E-BA可逆．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***102
2024-11-16 02:32:36
正确答案：证明 用反证法：若E-BA不可逆则|E-BA|=0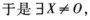
使得(E-BA)X=O→X=BAX．令Y=AX则X=BY→Y≠O(否则X=O)又(E-AB)Y=Y-ABY=Y-AX=O这与E-AB可逆矛盾故E-BA可逆．
证明用反证法：若E-BA不可逆,则|E-BA|=0,,使得(E-BA)X=O→X=BAX．令Y=AX,则X=BY→Y≠O(否则X=O),又(E-AB)Y=Y-ABY=Y-AX=O,这与E-AB可逆矛盾,故E-BA可逆．
相似问题
(A+B)2=A2+2AB+B2成立的充分必要条件是( )．A．B=EB．A=EC．AB=BAD．A
(A+B)2=A2+2AB+B2成立的充分必要条件是( )．A．B=EB．A=EC．AB=BAD．A=B请帮忙给出正确答案和分析，谢谢！
设A为n阶矩阵 将A的第i j行互换后再将第i j列互换得到矩阵B 则“A与B等价” “A与B相似”
设A为n阶矩阵，将A的第i，j行互换后再将第i，j列互换得到矩阵B，则“A与B等价”，“A与B相似”，“A与B合同”中成立的关系共有( )个．A．0B．1C．2D．3
设3阶矩阵A=(aij)的行列式|A|=2 设初等矩阵 试分别计算PiA与APi 并求det(Pi
设3阶矩阵A=(aij)的行列式|A|=2，设初等矩阵 试分别计算PiA与APi，并求det(PiA)与det(APi)的值，i=1，2，3．请帮忙给出正确答案和分析，谢谢！
设4阶方阵A＝设3阶方阵A B满足关系式：A－1BA＝6A＋BA 且A＝ 则B＝_______．设3
设4阶方阵A＝设3阶方阵A、B满足关系式：A－1BA＝6A＋BA，且A＝，则B＝_______．设3阶方阵A、B满足关系式：A－1BA＝6A＋BA，且A＝，则B＝_______．请帮忙
设设4阶方阵A的秩为2 则其伴随矩阵A*的秩为________．设4阶方阵A的秩为2 则其伴随矩阵A
设设4阶方阵A的秩为2，则其伴随矩阵A*的秩为________．设4阶方阵A的秩为2，则其伴随矩阵A*的秩为________．请帮忙给出正确答案和分析，谢谢！
