求对合的自对应元素的参数 这个对合由满足下列方程的对应点偶决定： (1)t2＝0与t2－3t＋1＝0

参考解答

490***102

2024-11-19 11:24:13



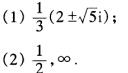
相似问题

• 证明：由平面上四个射影变换： 设G是全体实数的集合 证明：所有R的可以写成形如χ→aχ＋b(a b是

  证明：由平面上四个射影变换： 设G是全体实数的集合，证明：所有R的可以写成形如χ→aχ＋b(a、b是有理数设G是全体实数的集合，证明：所有R的可以写成形

• 求二阶曲线的方程 它是由下列两个成射影对应的线束构成的： (1)χ1－χ2－χ3＋λχ3＝0与χ1＋

  求二阶曲线的方程，它是由下列两个成射影对应的线束构成的： (1)χ1－χ2－χ3＋λχ3＝0与χ1＋2χ2－χ3＋λ′(χ1－4χ2＋χ3)＝0，且λ－λ′＝0 (

• 设平面丌内的点与平面π′内的直线的射影对应(对射对应)为： 求点P(1 2 1) Q(3 －1 2)

  设平面丌内的点与平面π′内的直线的射影对应(对射对应)为： 求点P(1，2，1)，Q(3，－1，2)，R(4，1，3)的像，并验证所对应的三直线共点．请帮忙给出正

• 求使A1(1 2 3) A2(2 －3 4) A3(4 5 －6) A4(11 9 －5) 分别对应

  求使A1(1，2，3)，A2(2，－3，4)，A3(4，5，－6)，A4(11，9，－5)，分别对应点B1(1，1，2)，B2(3，－2，4)，B3(5，3，－3)，B4(9，2，3)的射影变换，并且

• 设共线四点P1(3 1 －2) P2(1 3 1) P3(2 －2 －3) P4(1 －5 －4)

  设共线四点P1(3，1，－2)，P2(1，3，1)，P3(2，－2，－3)，P4(1，－5，－4)，求(P1P2，P3P4)．请帮忙给出正确答案和分析，谢谢！