设f(u v)具有连续偏导数 且满足fu(u v)+fv(u v)=uv求y(x)=e2x(x x)
设f(u,v)具有连续偏导数,且满足fu(u,v)+fv(u,v)=uv求y(x)=e2x(x,x)所满足的一阶微分方程,并求其通解.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:y'+2y=x2e2x;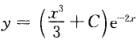 (c为任意常数).
(c为任意常数).
y'+2y=x2e2x;(c为任意常数).
相似问题
考虑二元函数的下面4条性质: ①f(x y)在点(x0 y0)处连续; ②f(x y)在点(x0 y
考虑二元函数的下面4条性质: ①f(x,y)在点(x0,y0)处连续; ②f(x,y)在点(x0,y0)处的两个偏导数连续; ③f(x0,y0)在点(x0,y0)处可微; ④f(x,
求二元函数z=f(x y)=x2y(4-x-y)在由直线x+y=6 x轴和y轴所围成的闭区域D上的极
求二元函数z=f(x,y)=x2y(4-x-y)在由直线x+y=6、x轴和y轴所围成的闭区域D上的极值、最大值与最小值.请帮忙给出正确答案和分析,谢谢!
*] 其中f和g具有二阶连续导数 求.请帮忙给出正确答案和分析 谢谢!
*],其中f和g具有二阶连续导数,求.请帮忙给出正确答案和分析,谢谢!
wps如何设置不同论文格式页码利用wps:如何设置不同格式页码呢?是否有简单易行的方法 可以帮助设置
wps如何设置不同论文格式页码利用wps:如何设置不同格式页码呢?是否有简单易行的方法,可以帮助设置论文排版,或者论文编写呢?
设函数f(x) g(x)均有二阶连续导数 满足f(0)>0 g(0)<0 且f(0)=g(0)=0
设函数f(x),g(x)均有二阶连续导数,满足f(0)>0,g(0)<0,且f(0)=g(0)=0,则函数z=f(x)g(x)在点(0,0)处取得极小值的一个充分条件是A.f"(0)<0,g"












