设n阶矩阵A满足A2=A 证明R(A)+R(E—A)=n 其中E为n阶单位矩阵．请帮忙给出正确答案和
设n阶矩阵A满足A2=A，证明R(A)+R(E—A)=n，其中E为n阶单位矩阵．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***101
2024-11-11 11:16:58
正确答案：称满足关系式A2=A的矩阵为幂等矩阵．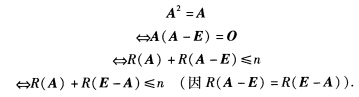
另一方面由矩阵秩的性质⑥知 R(A)+R(E一A)≥R(A+(E—A))=R(E)=n．综合以上两个不等式知R(A)+R(E—A)=n．
称满足关系式A2=A的矩阵为幂等矩阵．另一方面,由矩阵秩的性质⑥,知R(A)+R(E一A)≥R(A+(E—A))=R(E)=n．综合以上两个不等式知,R(A)+R(E—A)=n．
相似问题
若f(x)=-f(-x) 在(0 +∞)内f(x)＞0 f(x)＞0 则f(x)在(-∞ 0)内(
若f(x)=-f(-x)，在(0，+∞)内f(x)＞0，f(x)＞0，则f(x)在(-∞，0)内( )．A．f"(x)＜0，f""(x)＜0B．f"(x)＜0，f""(x)＞0C．f"(x)＞0．f""(x)＜0D．f"(x)
已知向量组 证明A组与B组等价．请帮忙给出正确答案和分析 谢谢！
已知向量组 证明A组与B组等价．请帮忙给出正确答案和分析，谢谢！
高100 cm的铅直水闸 其形状是上底宽200 cm 下底宽100 cm的梯形 求水闸上的压力：(1
高100 cm的铅直水闸，其形状是上底宽200 cm，下底宽100 cm的梯形，求水闸上的压力：(1)当水深50 cm时；(2)当水深100 cm时．请帮忙给出正确答案和分析，谢谢！
设三阶对称矩阵A的特征值为6 3 3 与特征值6对应的特征向量为p1=(1 1 1)T 求A．请帮忙
设三阶对称矩阵A的特征值为6，3，3，与特征值6对应的特征向量为p1=(1，1，1)T，求A．请帮忙给出正确答案和分析，谢谢！
用铁锤将一铁钉打入木板 设木板对铁钉的阻力与铁钉击入木板的速度成正比．在铁锤第一次打击时 能将铁钉击
用铁锤将一铁钉打入木板，设木板对铁钉的阻力与铁钉击入木板的速度成正比．在铁锤第一次打击时，能将铁钉击入木板内1 cm．如果铁锤每次打击所做的功相等
