如图1—5所示 一根绳子悬挂着小球在水平面内作匀速圆周运动 有人在竖直方向上求合力得出Tcosθ—m
如图1—5所示,一根绳子悬挂着小球在水平面内作匀速圆周运动,有人在竖直方向上求合力得出Tcosθ—mg=0,也有人沿绳子拉力方向求合力得出T一mgcosθ=0。显然两者不能同时成立,哪种正确,并说明理由。 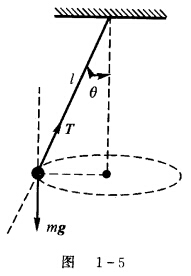
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:公式Tcosθ—mg=0是正确的。 小球受力如图1—5所示小球在水平面作匀速圆周运动向心加速度指向圆心向心力由重力和张力提供。由牛顿第二定律得T+mg=ma径向Tsinθ=man=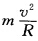 竖直方向了Tcosθ—mg=0。所以此式正确。而沿绳子方向分解也可以但在绳子的方向上是有加速度的其值为ansinθ。 绳子方向有T—mgcosθ=mansinθ垂直于绳子方向有mgsinθ=mancosθ将其简化可得Tsinθ=man。
竖直方向了Tcosθ—mg=0。所以此式正确。而沿绳子方向分解也可以但在绳子的方向上是有加速度的其值为ansinθ。 绳子方向有T—mgcosθ=mansinθ垂直于绳子方向有mgsinθ=mancosθ将其简化可得Tsinθ=man。
公式Tcosθ—mg=0是正确的。小球受力如图1—5所示,小球在水平面作匀速圆周运动,向心加速度指向圆心,向心力由重力和张力提供。由牛顿第二定律得T+mg=ma,径向Tsinθ=man=,竖直方向了Tcosθ—mg=0。所以此式正确。而沿绳子方向分解也可以,但在绳子的方向上是有加速度的,其值为ansinθ。绳子方向有T—mgcosθ=mansinθ,垂直于绳子方向有mgsinθ=mancosθ,将其简化可得Tsinθ=man。
相似问题
刚体绕定轴转动时 有人认为动能重力势能Ep=mghc 转动惯量J=mrc2 动量p=mvc 角动量L
刚体绕定轴转动时,有人认为动能重力势能Ep=mghc,转动惯量J=mrc2,动量p=mvc,角动量L=rc×mvc,式中m是刚体质量,vc是质心速度,|rc|是质心到转轴的距
1个轴承的直径。请帮忙给出正确答案和分析 谢谢!
1个轴承的直径。请帮忙给出正确答案和分析,谢谢!
现有两个测距仪 基线B分别为0.065m和1m 观察系统的视放大率分别为1×和20× 试分别求其测量
现有两个测距仪,基线B分别为0.065m和1m,观察系统的视放大率分别为1×和20×,试分别求其测量100m处的测量误差。请帮忙给出正确答案和分析,谢谢!
设绳上有两个相向传播的形状相同位移相反的脉冲波 当两波中心重合时合位移为零 那么波的能量到哪里去了?
设绳上有两个相向传播的形状相同位移相反的脉冲波,当两波中心重合时合位移为零,那么波的能量到哪里去了?请帮忙给出正确答案和分析,谢谢!
空气平板电容器 电容为C 与电压为u的电源相连 如图4-28所示。求两板间距慢慢地由d→nd过程中
空气平板电容器,电容为C,与电压为u的电源相连,如图4-28所示。求两板间距慢慢地由d→nd过程中,外力做的功。 请帮忙给出正确答案和分析,谢谢!












