设均匀细棒的质量为M 长度为L 其一端用铰链固定 另一端钉上一个质量为m的小球 如图5-7所示。现将
设均匀细棒的质量为M、长度为L,其一端用铰链固定,另一端钉上一个质量为m的小球,如图5-7所示。现将棒在水平位置无初速地释放。试求棒经过铅直位置时的角速度及角加速度。 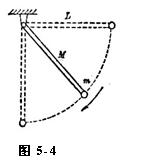
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:法一 利用刚体定轴转动的动能定理(或:机械能守恒定律)求解。刚体下摆过程中仅有重力做功根据动能定理可得 (1)求解式(1)可得角速度为
(1)求解式(1)可得角速度为 在铅直位置刚体所受力矩为零根据转动定律可得α=0
在铅直位置刚体所受力矩为零根据转动定律可得α=0 法二 利用对Z轴的角动量定理(或转动定律)求解。建立Z轴垂直纸面向里的坐标系X轴水平向右。棒的下摆为加速过程外力矩为重力对O的力矩。在棒上取质元dm当棒处在下摆角度θ时重力矩为M=∫gxdm (2)根据质心的定义∫xdm=mxC得到M=(M+m)gxc (3)而系统的质心坐标为
法二 利用对Z轴的角动量定理(或转动定律)求解。建立Z轴垂直纸面向里的坐标系X轴水平向右。棒的下摆为加速过程外力矩为重力对O的力矩。在棒上取质元dm当棒处在下摆角度θ时重力矩为M=∫gxdm (2)根据质心的定义∫xdm=mxC得到M=(M+m)gxc (3)而系统的质心坐标为 根据转动定律
根据转动定律 得到
得到 (4)将式(4)对角度θ积分得到
(4)将式(4)对角度θ积分得到 (5)求解式(5)得到
(5)求解式(5)得到 在铅直位置刚体所受力矩为零根据转动定律可得α=0
在铅直位置刚体所受力矩为零根据转动定律可得α=0
法一利用刚体定轴转动的动能定理(或:机械能守恒定律)求解。刚体下摆过程中,仅有重力做功,根据动能定理可得(1)求解式(1)可得角速度为在铅直位置,刚体所受力矩为零,根据转动定律可得α=0法二利用对Z轴的角动量定理(或转动定律)求解。建立Z轴垂直纸面向里的坐标系,X轴水平向右。棒的下摆为加速过程,外力矩为重力对O的力矩。在棒上取质元dm,当棒处在下摆角度θ时,重力矩为M=∫gxdm(2)根据质心的定义,∫xdm=mxC,得到M=(M+m)gxc(3)而系统的质心坐标为根据转动定律,得到(4)将式(4)对角度θ积分,得到(5)求解式(5)得到在铅直位置,刚体所受力矩为零,根据转动定律可得α=0
相似问题
初速度大小为v的子弹 垂直打穿一块木板后速度变为零 设木板对子弹的阻力是恒定的。求子弹射入木板厚度的
初速度大小为v的子弹,垂直打穿一块木板后速度变为零,设木板对子弹的阻力是恒定的。求子弹射入木板厚度的一半时子弹速度的大小(木板固定不动)。请帮忙
用角动量定理求出自由落体的加速度。请帮忙给出正确答案和分析 谢谢!
用角动量定理求出自由落体的加速度。请帮忙给出正确答案和分析,谢谢!
一列平面简谐波 沿X轴负向传播.角频率为ω 波速为u.设t=T/4时的波形如图7-7所示 则该波的表
一列平面简谐波,沿X轴负向传播.角频率为ω,波速为u.设t=T/4时的波形如图7-7所示,则该波的表达式为( ). A.y=Acosω(t-xu)B. C.y=Acos[ω(t+x
地球的自转角速度可以认为是恒定的.地球相对自转轴的转动惯量为9.8×1037kg·m2.则地球对自转
地球的自转角速度可以认为是恒定的.地球相对自转轴的转动惯量为9.8×1037kg·m2.则地球对自转轴的角动量为_______.请帮忙给出正确答案和分析,谢谢!
一个质量为m的小球自高度为y0 处沿水平方向以速率v0抛出.它与地面碰撞后跳起的最大高度(1/2)y
一个质量为m的小球自高度为y0,处沿水平方向以速率v0抛出.它与地面碰撞后跳起的最大高度(1 2)y0,水平速率为(1 2)0k,如图3-10所示.则碰撞过程中(1)地












